Angular Size Calculator
This Calculator Is Accurate For All Angles
Scroll Down For Instructions
Size and distance can be input in any units but they must be consistent.
If size is entered in inches, distance must be in inches.
If size is entered in kilometers, distance must be in kilometers, etc.
Examples for using this calculator:
1) A tennis ball is 2.5 inches in diameter. At what distance would it have to be so that it
would have the same angular size as the Moon (about 30 minutes of arc) ?
We want to solve for distance, so we click that button. Since we are going to
input the angle in minutes we click that button.
Input 30 minutes and 2.5 inches, click "calculate" and your answer is 286.48 inches.
Dividing this by 12, the answer is about 23.87 feet.
We also could have input .5 degrees and still arrived at the same answer.
|
| |
|
2) Mars was in the news recently due to its close approach to the Earth. Just how "big"
does Mars appear at its closest approach to the Earth?
We want to solve for angle, so we click that button. Now we need to know 2 things:
Mars closest approach to Earth is 35,000,000 miles and its diameter is 4,216 miles.
We enter these numbers, click "calculate" and our answer is .0069017 degrees, which is
an acceptable answer but in awkward units. Without re-inputting anything, just click
"minutes" and then click "calculate". Now our answer is .4141 minutes. Without re-inputting,
click "seconds" and then click "calculate". The answer is 24.846 seconds.
3) The Moon has an angular size of 30 minutes and its distance from the Earth is about
240,000 miles. What is its diameter?
We are solving for size and so we click that button. Then since we need to input angle
in minutes we click that button. We enter the numbers in the appropriate boxes and we
get an answer of 2,094.4 miles.
Angular Size Tutorial
When trying to describe the size of an object (especially
an object in the sky), it is difficult for the average person to do this precisely.
You could
say that the Moon looks to be about the size of a tennis ball but that isn't very specific.
Do you mean a tennis ball as seen from a foot ? 5 feet? 10 feet? 100 feet?
In order to express this properly, you would have to describe the object in terms of its angular
size. As we saw in example 1, the Moon's angular size is 30 minutes of arc which is
about the same size that a tennis ball appears at 24 feet.
|
| |
|
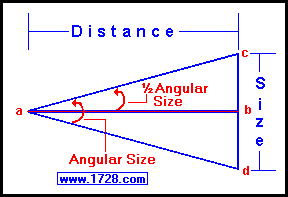
From trigonometry we can derive a simple formula that works for small angles
only. Looking at the diagram at the top of the page, we could take triangle
ACD as a right triangle (which it isn't) with the 90 degree angle as CDA. Line CD is the
size of the object, Line AD is the distance and CAD is the angle.
We then can generate a simple angular size formula
tan (angle) = opposite/adjacent = Line CD/ Line AD = size/distance
Since this works for small angles, let us take the tangent of 1 degree which is .017455
which means that when an object's size is .017455 times its distance, it has an angular
size of 1 degree. OR to put it another way: When an object's distance is 57.29 times its
size, it has an angular size of 1 degree.
Multiplying 57.29 by 60 minutes per degree we get 3,437.4 which means that an object
at a distance of 3,437.4 times its size will have an angular size of 1 minute.
Multiplying 57.29 * 3,600 seconds per degree we get 206,244 meaning an object at a
distance of 206,244 times its size displays an angular size of 1 second.
We can generate another simple formula:
Angular size in degrees = (size * 57.29) / distance
No doubt you can figure out the formulas for minutes and seconds of arc.
As stated previously, the simple formulas only work for small angles.
The formulas for angular sizes up to 180 degrees are a little more complex but you don't
have to be concerned about this because this calculator is valid for angular sizes up to
180 degrees.
Numbers are displayed in scientific notation with the option to specify the precision by
inputting a number in the box above. For easy readability, numbers between .001 and
1,000 will not be displayed in scientific format.
Internet Explorer and most other browsers, will display the numbers properly but
there are a few browsers that will show no output whatsoever. If so, enter a zero
in the box above. This eliminates all formatting but it is better than seeing no
output at all.
|