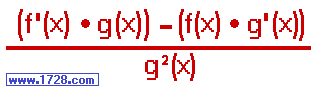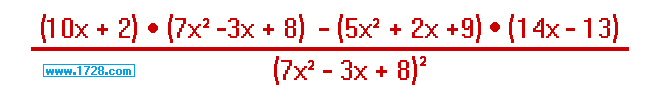Product Rule
Quotient Rule
and Chain Rule
Product Rule
Derivative of f(x) • g(x) = (f '(x) • g(x)) + (f(x) • g'(x))
EXAMPLE
: The derivative of
(x³ + 5x² -6x + 9) • (7x³ -x² -8x + 1)
Equals
(3x² + 10x -6)•(7x³ - x² -8x + 1) +
(x³ + 5x² -6x + 9)•(21x² -2x -8)
Quotient Rule
Derivative of f(x) ÷ g(x) equals
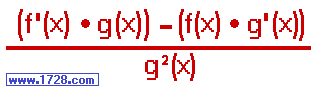
EXAMPLE
: The derivative of
(5x² + 2x + 9)
(7x² -3x + 8)
equals
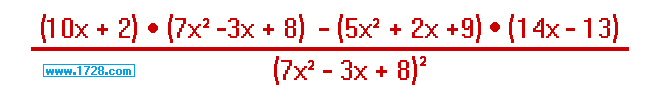
Chain Rule
First, we should discuss the concept of the composition of a function
which actually means the function of another function.
It is easier to discuss this concept in informal terms.
ALL compositions of 2 functions consist of 2 parts:
1) The function inside the parentheses and
2) The function outside of the parentheses.
As an example, let's analyze 4•(x³+5)²
Speaking informally we could say the "inside function" is (x3+5) and
the "outside function" is 4 • (inside)2.
Before using the chain rule, let's multiply this out and then take the derivative.
4 • (x3+5)2 = 4x6 + 40 x3 + 100
derivative = 24x5 + 120 x2
Now, let's differentiate the same equation using the
chain rule which states that the
derivative of a composite function equals:
(derivative of outside) • (inside) • (derivative of inside).
Using the chain rule to differentiate 4 • (x3+5)2 we obtain:
derivative of outside = 4 • 2 = 8
inside = x3 + 5
derivative of inside = 3x2
Now we multiply all 3 quantities to obtain:
ANSWER = 8 • (x3+5) • (3x2)
As a double check we multiply this out and obtain:
8x3+40 • (3x2) = 24 x5 + 120 x2 which is precisely
the answer we obtained by using the "long way".
By now you might be thinking that the problem could have been solved with or without the
chain rule. However, let's take a more complex example:
EXAMPLE: What is the derivative of
(4X3 + 5X2 -7X +10)14 ?
ANSWER: 14 • (4X3 + 5X2 -7X +10)13• (12X 2 + 10X -7)
Yes, this problem could have been solved by raising (4X3 + 5X2 -7X +10) to
the fourteenth power and then taking the derivative but you can see why the
chain rule saves an
incredible amount of time and labor.
And yes, 14 • (4X3 + 5X2 -7X +10)13• (12X 2 + 10X -7)
is an acceptable answer. After all, once we have determined a derivative, it is much more
convenient to "plug in" values of x into a compact formula as opposed to using some multi-term
monstrosity.
The chain rule can also help us find other derivatives.
For example, what is the derivative of the
square root of (X3 + 2X + 6) OR (X3 + 2X + 6)½ ?
ANSWER: ½ • (X3 + 2X + 6)-½ • (3X2 + 2)
Another example will illustrate the versatility of the chain rule.
Let's introduce a new derivative
if f(x) = sin (x) then f '(x) = cos(x)
Now we can solve problems such as this composite function:
what is the derivative of sin(5x3 + 2x) ?
ANSWER: cos(5x3 + 2x) • (15x2 + 2)
The chain rule is a powerful tool of calculus and it is important that you understand it
thoroughly.
_____________________
RETURN TO CALCULUS
INDEX
Return To Home Page
Copyright © 1999 -
1728 Software Systems
|