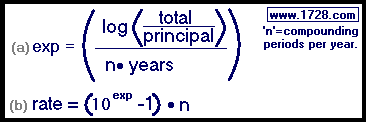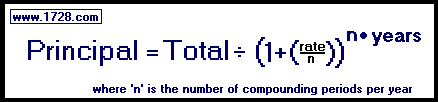* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * You have $1,200 in a savings account with an interest rate of 7 per cent compounded semi-annually. How much money do you have after 5 years? Total = 1,200 * (1+.[07 ÷ 2])2•5 Total = 1,200 * (1.035)10 Total = 1,200 * 1.4105987606 Total = 1,692.72

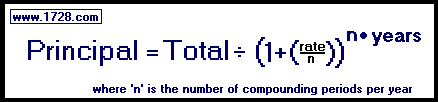
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * After 10 years in a 6% compounded quarterly savings account, you have $18,140.19. What amount was invested originally? Principal = $18,140.19 ÷ (1 + [.06÷2])4•10 Principal = $18,140.19 ÷ 1.01540 Principal = $18,140.19 ÷ 1.8140184087 Principal = $10,000.00

* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * $10,000 invested in a 10% compounded monthly account eventually yields $15,000. How many years did this take? Years = log(15,000 ÷ 10,000) ÷ 12*log(1 + (.1/12)) Years = log(1.5) ÷ 12*log(1.00833333333333) Years = 0.176091259055681 ÷ 12*0.003604124268825 Years = 4.07152209342589 * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *

          Revised August, 2014
           

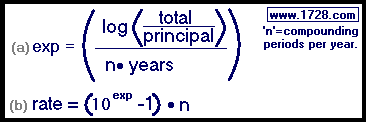
After 12 years an initial deposit of $15,000 yields $50,000 in a compounded daily account.
What was the daily rate of this investment?

Using equation (a) ('exp' means exponent)
exp = {log(total ÷ principal)} ÷ n • years
exp = {log(50,000 ÷ 15,000)} ÷ 365 • 12
exp = {log(3.33333333333)} ÷ 4,380
exp = {0.52287874528} ÷ 4,380
exp = 0.000119378708968114

Inserting the exponent into equation (b):
rate = (10^exponent -1) • n
rate = (10^{0.000119378708968114} -1) • 365
rate = (1.00027491741856 -1) • 365
rate = (.00027491741856) • 365
rate = 0.10034485777428

Multiplying this by 100 to get a percentage:
rate = 10.034485777428%