EXPONENTIAL GROWTH CALCULATOR

Exponential Growth Calculator
Based on common logs and base 10 exponents
To see exponential growth based on natural logs and the exponent "e", click here.
To read about exponential decay particularly half-life, click here.

The above formulas are used in calculations involving exponential growth.

This calculator can solve exponential growth problems whenever three of the four variables are known:
• beginning amount
• ending amount
• rate
• time

There are four exponential growth problems further down this page.

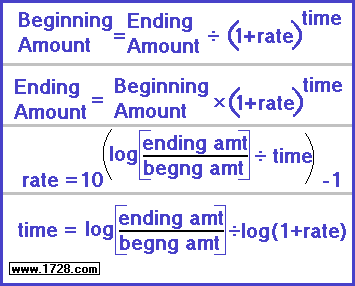
Using the calculator is quite simple:
• Click the variable for which you are solving.
• Enter the appropriate numbers in the 3 input boxes
• Click "CALCULATE" for the answer

Do you want to solve for:

1) After 5 hours, a bacteria culture with a growth rate of 30% per hour has grown to a population of 70,000.
What was the bacteria population at the beginning of the experiment (five hours ago.)?

Beginning Amount = Ending Amount ÷ (1 + rate)^time

Beginning Amount = 70,000 ÷ (1.3)⁵

Beginning Amount = 70,000 ÷ 3.71293

Beginning Amount = 18,853

* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *

2) In 2010, a city had a population of 441,000.
In 2020, it had a population of 450,000.
What was its population in 2018?

We first have to calculate the annual population growth rate.
Fram 2010 to 2020, the city's population increased by a factor of 1.0204081633
(which is 450,000 divided by 441,000.)
We can calculate the annual growth rate with this equation:

(1 + population rate)^10 years = (growth factor)

We then solve the equation by taking logs of both sides which yields:
10 * (1 + population rate) = log (1.0204081633)

(1 + population rate) = 0.0087739243223 ÷ 10

Looking up the anti-log of 0.00087739243223 we get:

1.0020223129 which is the annual growth rate.

We raise this number to the 8th power and then multiply it by the 2010 population:

(1.0020223129)^8 * 441,000
and this equals: 448,185, the 2018 population.

* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *

3) You have a bank account which doubles your money every 9 years.
What is the annual interest rate of this account?

Rate = 10^{(log[Ending Amount / Beginning Amount] ÷ time)} -1

We don't have actual numbers so we will substitute 1,000 for beginning amount and 2,000 for ending amount.

Rate = 10^{(log[2,000 / 1,000] ÷ 9)} -1

Rate = 10^{(0.301029995663981 ÷ 9)} -1

Rate = 10^{(0.0334477772959979)} -1

Rate = 8.005973889231%

* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *

4) A bacteria culture begins with a population of 7,000 and increases to 13,026 after 3 hours.
How long will it take the population to triple? (That is, when will the population be 21,000?)

We first must solve for the rate.
Rate = 10^{(log[Ending Amount / Beginning Amount] ÷ time)} -1

For every 3 hours, we see that the population increases by a factor of 13,026 / 7,000

Rate = 10^{(log[13,026 / 7,000] ÷ 3)} -1

Rate = 10^{(log[1.86085714285714] ÷ 3)} -1

Rate = 10^{(0.2697130338238070 ÷ 3)} -1

Rate = 0.229997828197444

Now, we can solve for the time.

Time = log(ending amount / beginning amount) ÷ log (1 + rate)

Time = log(21,000 / 7,000) ÷ log (1.229997828197444)

Time = 0.477121254719662 ÷ 0.0899043446079357

Time = 5.30698774125259

If we were to solve this problem using the calculator, we would first click the rate function, enter the numbers, and then use this rate calculation after we click the time function.

The default setting is for 5 significant figures but you can change that by inputting another number in the box above.

Answers are displayed in scientific notation and for easier readability, numbers between .001 and 1,000 will be displayed in standard format (with the same number of significant figures.)
The answers should display properly but there are a few browsers that will show no output whatsoever. If so, enter a zero in the box above. This eliminates all formatting but it is better than seeing no output at all.

Return To Home Page