Bicyclists, motorists, carpenters, roofers and others either need to calculate slope or at least must have some understanding of it.
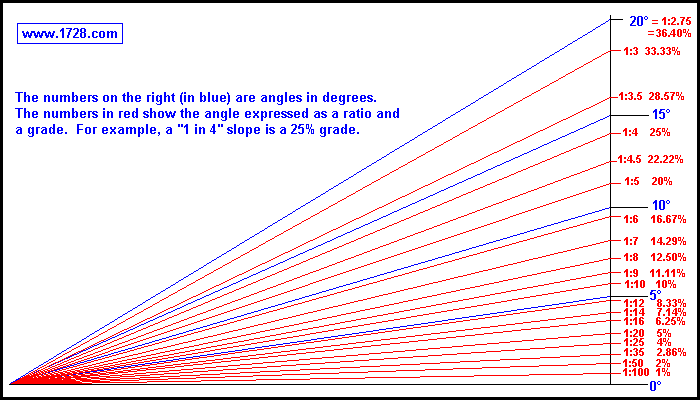
Slope, tilt or inclination can be expressed in three ways:
1) As a ratio of the rise to the run (for example 1 in 20)
2) As an angle (almost always in degrees)
3) As a percentage called the "grade" which is the (rise ÷ run) * 100.

Of these 3 ways, slope is expressed as a ratio or a grade much more often than an actual angle and here's the reason why.
Stating a ratio such as 1 in 20 tells you immediately that for every 20 horizontal units traveled, your altitude increases 1 unit.
Stating this as a percentage, whatever horizontal distance you travel, your altitude increases by 5% of that distance.

Stating this as an angle of 2.8624 degrees doesn't give you much of an idea how the rise compares to the run.

Calculating Grade From A Map One way to calculate the grade of a hill is with a map that shows the altitudes of locations. For example, you've measured out a distance of 3 miles (run) with a change in altitude of 396 feet (rise). First, the units must be made consistent, so we convert 3 miles to 15,840 feet. grade = (rise ÷ run) * 100 grade = (396 ÷ 15,840) * 100 = 2.5%

With an altimeter and an odometer, we travel the exact route we measured on the map and our altimeter indicates a change in altitude of 396 feet which, not surprisingly, is precisely what we had already measured on the map. However there is a small difference between the 3 mile distance measured on the map and the 3.0009375 miles (15,844.95 feet) we just traveled on the road. The map distance is the true horizontal distance but the travel distance of 3.0009375 miles is the slope length or slope distance. To calculate the true run, we need to use the Pythagorean Theorem.
run = Square Root (15,844.95² - 396²) run = 15,840 feet Now we can calculate the grade = (396 ÷ 15840) * 100 = 2.5%
The slope angle exactly equals what we previously calculated because instead of using the slope length as the run, we used it to calculate the true horizontal distance.

Calculating Grade By Using Slope Distance If we calculate slope from the formula: grade = (rise ÷ slope length) * 100 we must remember that this is not the proper way to do so and it is not the method we learned in algebra class. However, it does have the advantage that it is usually easier to find a slope length than the horizontal run and it is fairly accurate when the angles are 10 degrees and smaller.
So, returning to the previous problem, we could calculate the grade as (396 ÷ 15,844.95) * 100 which equals 2.49922% and since we are dealing with a small angle, it is very close to the actual figure of 2.5%.
As the angles get larger, the calculations start to diverge dramatically.

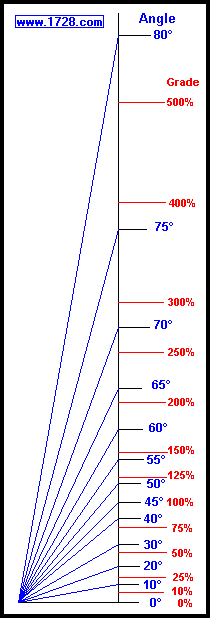
Look at the table below.
Column 1 is the angle in degrees.
Column 2 is the rise over run percentage for that angle. (The trigonometric definition for column 2 is the tangent of that angle times 100. It is also the grade for that angle.)
Column 3 is the rise over slope length (or hypotenuse) percentage for that angle. (or sine of that angle times 100).
Column 4 is the percentage amount of how much larger column 2 is than column 3.

1   Angle	2     % rise / run	3     % rise / hyp	4   % Diff
5	8.74887	8.71557	100.3820
10	17.63270	17.36482	101.5427
15	26.79492	25.88190	103.5276
20	36.39702	34.20201	106.4178
25	46.63077	42.26183	110.3378
30	57.73503	50.00000	115.4701
35	70.02075	57.35764	122.0775
40	83.90996	64.27876	130.5407
45	100.00000	70.71068	141.4214
50	119.17536	76.60444	155.5724
55	142.81480	81.91520	174.3447
60	173.20508	86.60254	200.0000
65	214.45069	90.63078	236.6202
70	274.74774	93.96926	292.3804
75	373.20508	96.59258	386.3703
80	567.12818	98.48078	575.8770
85	1,143.00523	99.61947	1,147.3713
90	Infinite	100.00000	Infinite

As can be seen, when angles are as large as 10 degrees, using slope length for calculations starts generating errors of about 1½ per cent so, it would be wise to use 10 degrees as the upper limit for the "rise to slope length" calculations.

This table is convenient for viewing the grade of various angles. For example, a 10 degree angle has a 17.63270% grade. It's interesting to see that a 45 degree angle has a 100% grade.

Measuring Slope Directly

Instead of determining slope by measuring distances we can measure it directly. There are tools (inclinometers) which measure slope, tilt, etc. Of course if we use one of these, it is a good idea to take more than one measurement and at different locations. For example, on that 3 mile stretch of road, it is highly unlikely that it is a 2.5% grade at every single point. So, using an inclinometer at several locations and then calculating an average of those measurements would yield a much better indication of the road's slope.

Another way to determine slope is with a level. Roofers (among others) use this method.
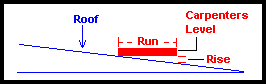One end of the level is placed along the slope of a roof and the lower end is lifted until the bubble indicates it is perfectly horizontal. The rise is then measured. Roofers and carpenters generally use a 1 foot level and the rise is measured in inches and so the slope of the roof (or pitch as they call it) is stated as inches per 12 inches. So, the pitch of a roof can be 1 in 12, 2in 12, and so on.

Wheelchair Ramps Besides roads and roofs the concept of slope is quite essential in the design of wheelchair ramps. For this purpose, the slope should never be greater than 1 in 12. In designing a wheelchair ramp for the elderly, a gentler slope of 1 in 18 should be considered.
If the ramp will be exposed to the weather, icy conditions should be taken into account for safety.

Formulas Showing Grade, Ratio & Angle Relationships

1) If we know the ratio of a road or highway (for example 1 in 20), then
  angle A = arctangent (rise ÷ run) which equals
  arctangent (1 ÷ 20) =
  arctangent (.05) =
  2.8624 degrees and the

  grade = (rise ÷ run) * 100 which equals
  (1 ÷ 20) * 100 =
  5%.

2) If we know the angle of a road or highway (for example 3 degrees) then the
  ratio = 1 in (1 ÷ tan (A)) which equals
  1 in (1 ÷ tan (3)) =
  1 in (1 ÷ .052408) =
  1 in 19.081 and the

  grade = (rise ÷ run) * 100 which equals
  (1 ÷ 19.081) * 100 =
  5.2408%

3) If we know the grade of a road (for example 3%), then
  angle A = arctangent (rise ÷ run) which equals
  arctangent (.03) =
  1.7184 degrees and the

  ratio = 1 in (1 ÷ tan(A)) which equals
  1 in (1 ÷ tan(1.7184)) =
  1 in (1 ÷ .03) =
  1 in 33.333

C A L C U L A T O R     I N S T R U C T I O N S This calculator computes slope as rise over run (first output row) and slope as rise over slope length (second output row).
Let's use some previous calculations as examples:
396 foot rise 15,840 foot run 15,844.95 foot slope length
2.5% grade 1.4321 degree angle 1 in 40 ratio

1) Click on ratio. Input 396 rise and 15840 run, then click calculate.
Since we have input the true horizontal run, we read the first output line
1.4321 degrees and 2.5% grade.
Entering 396 rise and 15844.95 run, (which is actually the slope length)
we read the second output row and see the results are 1.4321 degrees and 2.5% grade which is exactly what they should be. The third row shows the calculation of the true horizontal run which is 15840 feet.

2) Click on angle. Input 1.4321 and click calculate.
Since this angle was computed by a true rise to run ratio, we read the first output row of 1 in 40 ratio and 2.5% grade.

3) Click on grade. Input 2.5 and then click calculate.
The answers are 1 in 40 ratio and 1.4321 degrees.
Let's suppose we are entering a grade that was computed by rise over slope length.
Enter 2.44992 and reading the second output line we see this yields a 1 in 40 ratio and a 1.4321 degree angle.

The graph at the top of this page shows a small range of angles from zero to 20 degrees.
The chart below covers a wider range of angles:

---

Significant Figures >>>

Answers are displayed in scientific notation with the number of significant figures you specify in the box above.
For easier readability, numbers between .001 and 1,000 will not be in scientific notation.
Most browsers, will display the answers properly but there are a few browsers that will show no output whatsoever. If so, enter a zero in the box above which eliminates all formatting but it is better than seeing no output at all.

---

Return To Home Page

Copyright © 2000   1728 Software Systems