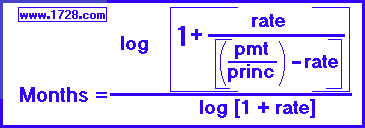
Here, the loan formula has been solved for months.
As you can see from the above formula, solving for months is a bit trickier than solving for monthly payment or principal.
We need to take a loan for $50,000 and we can afford to pay $800.00 per month. The local bank charges 9 per cent interest.
How much time will it take to repay this loan?
1) The rate would be 9 ÷ 1,200 = .0075
2) The principal is $50,000.00
3) The monthly payment is $800.00
|
|