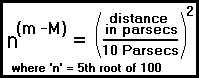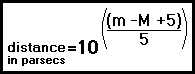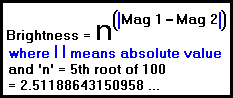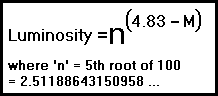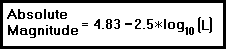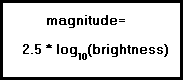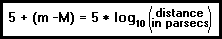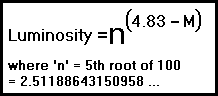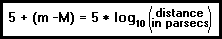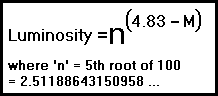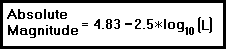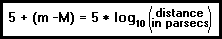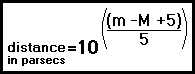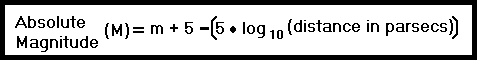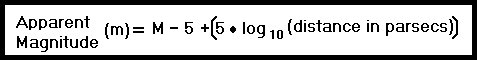Advanced Magnitude
Calculator & Tutorial
For a simpler magnitude calculator, click here.
|
The advanced magnitude calculator can do the same calculations as the previous one along with six additional functions.
Also, the tutorial discusses magnitude in greater detail and shows formulas, procedures and has eight examples involving magnitude calculations.
|
| |
Calculator Instructions
You have a choice of 9 different calculations. Look at the abbreviations to see what each button does.
For example, to make an Absolute Magnitude to Luminosity calculation, click button #3, enter the data and then click "Calculate".
The button numbers correspond to the nine example problems further down the page.
The "light years" and "Parsecs" buttons are for input only. Whenever distance is calculated, it will always be shown in light years and parsecs.
|
| |
Abbreviations used:
M = absolute magnitude L = luminosity
m = visual magnitude d = distance in light years
|
| |
Magnitude Tutorial
Apparent Magnitude
The system of classifying stars by their brightness originated with the Greek astronomer Hipparchus (190 BC - 120 BC) who categorized stars into six magnitudes, the brightest were classified as magnitude 1 and the stars just barely visible to the human eye were designated as magnitude 6.
In the nineteenth century, the British astronomer Norman Pogson (1829 - 1891) proposed a system in which a difference of five magnitudes would be exactly equal to 100. Also, with more modern methods of determining brightness, some stars' magnitudes had to be adjusted to fit into the new system.
So, in astronomy, brightness is expressed in magnitudes with each magnitude change equal to the 5th root of 100 or 2.5119 or a more exact figure of:
Also, the brighter an object the smaller the magnitude and the dimmer an object the larger the magnitude.
Apparent (or visual) magnitude is based upon an object's brightness as it appears from Earth.
Inverse Square Law
A very important concept in astronomy, physics and a great many other studies, is the inverse square law which states that when a force (such as gravity) or a type of energy (such as light) radiates from a source, its intensity is inversely proportional to the square of the distance from the source. For example the Earth is one astronomical unit of distance from the Sun. If it were at 2 astronomical units, then the Sun would be one quarter (½)² as bright, at three astronomical units it would be one ninth (⅓)² as bright.
Absolute Magnitude
Having just discussed apparent magnitude, there is another type called absolute magnitude which is based upon an object's true or intrinsic brightness. The Sun has an extremely bright magnitude but this is due to the fact that it is very close to the Earth. If all stars were to be seen at the same distance, then the ONLY factor affecting its magnitude would be its intrinsic brightness.
Astronomers have chosen the distance of ten parsecs (32.6156 Light Years) as the arbitrary point at which all stars would be compared.
Every star that is less than 10 parsecs from the Earth will always have an apparent magnitude that is brighter than its absolute magnitude (if m < M, distance < 10 parsecs).
Every star that is greater than 10 parsecs from the Earth will always have an absolute magnitude that is brighter than its apparent magnitude (if m > M, distance > 10 parsecs).
Luminosity
Luminosity is another way to express brightness. Here the Sun is given the arbitrary value of 1 and a star twice as bright as the Sun has a luminosity of 2 and a star that is half as bright as the Sun has a luminosity of .5 and so on.
As is the case with absolute magnitude, luminosity is also based strictly on the object's actual (or intrinsic) brightness and the object's distance has nothing to do with it. This is similar to the way in which a light bulb's brightness is rated. A 100 watt bulb looks very bright when it is just a few feet away but if your neighbor down the street is lighting his porch with a 100 watt bulb, it looks a heck of a lot dimmer doesn't it? Nonetheless, they are both 100 watt bulbs and have equal brightness or luminosity.
Since absolute magnitude and luminosity are both based on a star's actual or intrinsic brightness, if you know one, you can calculate the other. (See examples 2 & 3).
Magnitude Formulas
Now that we have the necessary definitions, we can derive some magnitude formulas.
Yes, we could easily look up these formulas, but it might be helpful to see how they are generated.
(If not, you can always use the calculator.)
From the definitions we learned that raising the 5th root of 100 to the power of the magnitude is the way in which brightness can be compared. For example, a second magnitude star is 15.85 times brighter than a fifth magnitude star. (2.5119³ = 15.85)
We know a star's brightness as observed from ten parsecs is defined as its absolute magnitude.
From the inverse square law, we know that brightness decreases by the square of the distance.
Knowing these relationships, we can set up a formula:
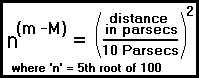We'll have to use a little algebra to make that formula more user-friendly:
Multiplying both sides by 10 parsecs squared we have:
100 • (n)(m -M) = distance²
taking the log10 of both sides:
2 + (m -M)• log10 (2.511886...) = 2 • log10 (distance)
The log10 (2.511886...) = .4 exactly:
2 + (m -M) • .4 = 2 • log10(distance)
Multiplying both sides by 2.5 yields:
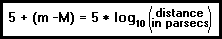
That's a much easier formula to manipulate isn't it?
Dividing both sides by 5 we obtain:
(5 + (m - M)) ÷ 5 = log10(distance in parsecs)
Exchanging the left and right hand sides of that equation produces:
log10(distance in parsecs) = 5 + (m - M)
5
Raising both sides of the equation to the power of ten, the left side of the equation is
now 10log10 (distance) which simply becomes
distance. We will keep the right side equation raised to the power of ten and the equation is now:
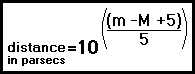
9 Magnitude Problems
Remember that these problems are numbered to correspond with the nine calculator buttons.
1) The star Sirius has an apparent magnitude of -1.46 and the star Regulus has an apparent magnitude of 1.36 How much of a brightness difference is this?
To calculate the brightness difference we'll need to use this formula:
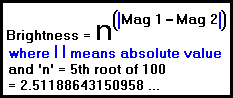magnitude1 - magnitude2 = | 1.36 - (-1.46) | = 2.82
Designating the 5th root of 100 as 'n' and raising it to the power of the magnitude difference we calculate:
brightness = n2.82 = 13.428
Rounding down to 3 significant figures, this means that Sirius is 13.4 times brighter than Regulus.
1b) The variable star Mira has been observed from a maximum brightness of magnitude 2.0 down to an extremely faint magnitude 10.1.
How much of a brightness change is that?
| 10.1 - 2.0 | = 8.1 magnitudes
brightness = n8.1 = 1,737.8
Rounding that to 2 significant figures makes this a brightness change of 1,700.
2) A brightness change of 30 equals how much of a change in magnitude ?
To calculate the magnitude change we'll start with a formula similar to the one shown in example 1.
(2.511886...)magnitude = brightness
Taking logs of both sides we get:
magnitude * log (2.511886...) = log (brightness)
Solving for magnitude:
magnitude = log (brightness) ÷ .4
Returning to our problem, we must calculate 30 brightness units in terms of magnitude.
magnitude = log (30) ÷ .4
magnitude = 1.477121255 ÷ .4
magnitude = 3.6928
3) The star Vega has an absolute magnitude ('M') of 0.58 what is its luminosity?
Absolute Magnitude and Luminosity are directly related but we have to see precisely how.
We will have to change the brightness formula from example 1.
We can use 'Luminosity' instead of the word 'Brightness' and we'll look up the absolute magnitude of the Sun which is 4.83.
A star of absolute magnitude 3.83 would be about 2.5119 times (one magnitude) brighter than the Sun and
a star of absolute magnitude 2.83 would be 6.31 times (two magnitudes or n²) brighter and so on.
As can be seen, to calculate the luminosity, we raise the 5th root of 100 to the power of the magnitude difference and the formula is:
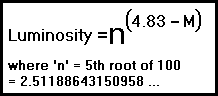Since Vega is 4.25 magnitudes brighter (4.83 - 0.58) than the Sun, it has a luminosity of n4.25 which equals 50.119 or 50.1 to 3 significant figures.
4) The star Altair has a luminosity ('L') of 11. What is its absolute magnitude?
To generate a formula, we take the logarithm of the formula from example 2:
log10 (Luminosity) = (4.83 - Absolute Magnitude) * log10(n)
log10 (Luminosity) = (4.83 - Absolute Magnitude) * .4
2.5 * log10 (Luminosity) = (4.83 - Absolute Magnitude)
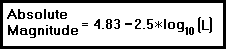Entering 11 into the above formula, we have:
Absolute Magnitude = 4.83 -2.5*log10 (11) = 4.83 -2.5*(1.0414) = 4.83 -2.603 = 2.23
5) Measured from the Earth, the Sun has an apparent magnitude of -26.74 and is 4.848 x 10-6 parsecs distant. What would be its magnitude if it were 10 parsecs away?
Basically, this question is asking us to determine the absolute magnitude of the Sun and even though we already looked it up, let's try calculating it.
At 10 parsecs, the Sun is going to be much dimmer than when it was at one astronomical unit.
Using the inverse square law, we'll have to divide the Sun's present distance by 10 parsecs and square the result:
(4.848137 x 10-6 parsecs ÷ 10 parsecs)2
equals 2.3504 x 10-13 which means the Sun's absolute magnitude is going to be considerably dimmer than its apparent magnitude. We learned from example 1 that:
Brightness = n(magnitude)
In order to use this formula, we will have to take logarithms of both sides.
log (Brightness) = magnitude * log (n)
The log of the 5th root of 100 is .4 and so:
log (Brightness) = magnitude * .4
magnitude = log (Brightness) / .4 Or
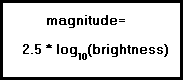magnitude = 2.5 * log (2.350443 x 10-13)
magnitude = 2.5 * -12.62885
magnitude = -31.57213
That number represents how much dimmer the Sun will be at 10 parsecs.
So to calculate the Sun's absolute magnitude, we subtract that number from its apparent magnitude:
-26.74 - -31.57213 = -26.74 +31.57213 which equals 4.83
Wow, that's a lot of work. How about using the formula we generated?
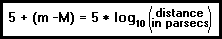
This formula can easily be solved for absolute magnitude:
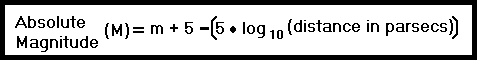
M = m +5 -[5 • log10(distance)]
M = -26.74 +5 -[5 • log10 (4.848 x 10-6)]
M = -21.74 -(5 • -5.3144)
M= -21.74 +26.572
Sun's Absolute Magnitude = 4.83
Well, that was a lot easier and of course, it's even easier just to use the calculator.
6) The star Sirius has an absolute magnitude ('M') of 1.45 and is 8.60 light years (2.64 parsecs) away. What is its luminosity and apparent magnitude?
The first part of the question can be solved with the absolute magnitude to luminosity formula:
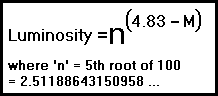
Luminosity = n(4.83 -1.45) = n(3.38) = 22.5
To solve for apparent magnitude, we could use the inverse square law but as we saw in example 4, it's a lot easier to use the formula we generated:
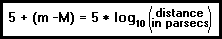
Which can easily be solved for apparent magnitude:
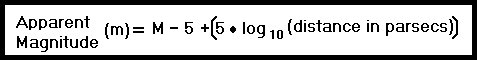
m = M - 5 + [5 • log10(distance)]
m = 1.45 -5 + [5 • log10(2.64 parsecs)]
m = -3.55 + 5 • .422
Apparent Magnitude = -1.44
7) The star Capella has an absolute magnitude ('M') of -.48 and an apparent magnitude of .08. What is its luminosity and distance?
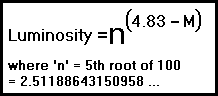
Luminosity = n(4.83 -M) = n5.31= 133.05 = 133
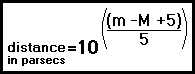
distance = 10(-.48 -.08 +5) ÷ 5
distance = 10(4.44) ÷ 5
distance = 10(.888)
distance = 12.9 parsecs = 42.2 light years
8) The star Wolf 359 has a luminosity of .00002 and is 7.78 light years (2.39 parsecs) distant. What is its apparent and absolute magnitude?
We'll use the luminosity to absolute magnitude formula:
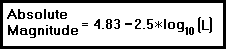
M = 4.83 - 2.5 • log10(luminosity)
M = 4.83 - 2.5 • log10(.00002)
M = 4.83 - 2.5 • log10(.00002)
M = 4.83 - 2.5 • (-4.70)
M = 4.83 - (-11.75)
Absolute Magnitude = 4.83 + (11.75) = 16.58
and for calculating the apparent magnitude:
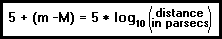
m = M + 5 • log10(distance in parsecs) -5
m = M + 5 • log10(2.39) -5
m = 16.58 + (5 • .3784) -5
m = 16.58 + (1.89) -5
Apparent Magnitude = 13.47
9) You are travelling in outer space and you measure the Sun's magnitude to be 2.75. How far away from the Sun are you?
We already know the Sun's absolute magnitude is 4.83.
Since we observed the Sun at magnitude 2.75, that means its apparent magnitude
is 2.75.
As for solving for distance, we'll use:
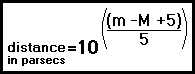
distance = 10((2.75 -4.83 +5) ÷ 5)
distance = 10((2.92) ÷ 5)
distance = 10(.58)
distance = 3.84 parsecs = 12.5 light years
|