Calculus - Calculating Minimum and Maximum Values Part I

Calculus - Determining
Minimum & Maximum Values
Part I

One of the most important uses of calculus is determining minimum and maximum values. This has its applications in manufacturing, finance, engineering, and a host of other industries. Before we examine a real-world example, we should learn how to calculate such values.

Let's use for our first example, the equation 2X² -5X -7 = 0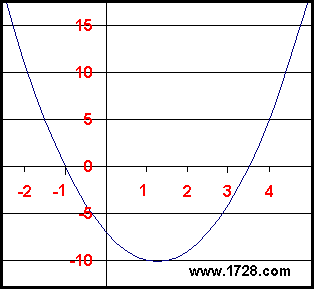

This is a quadratic equation in one variable. That is to say it is an equation of the form: ax² + bx + c = 0
With equations of this type, we know that when the "a" term is positive, the graph of the curve will be "concave up" (U-Shaped) and therefore the equation will have a minimum value but no maximum value (okay - technically, the maximum value is infinity). Looking at the graph we see that the minimum point is roughly X = 1.5 and Y = -10. Is there a way to determine the minimum point without graphing the equation and getting an exact value? Yes there is !

Look at the graph. If slope values were calculated for points on the left side of the curve, you could see that the slope would always be negative but it becomes "less negative" the closer the curve approaches the minimum (the bottom). If the slope were calculated along the right side of the curve, the value would always be positive and the slope values would get larger the further away from the "bottom" the points were.

So, it is logical to think that the slope is zero at that "bottom" point and therefore the derivative is zero at that point too.
So, let's take the derivative of 2X² -5X -7 = 0 which is:

4X - 5 When 4X -5 equals zero, X =1.25 which means that at this point, a minimum value exists. As for the 'Y' value, we go to the original equation and enter the value of X as 1.25. Y = 2X² -5X -7 Y = 2*(1.25)² -5*1.25 -7 Y = -10.125 So, at point X=1.25, Y= -10.125 there exists a minimum value.

In this example we knew that we were obtaining a minimum value because we graphed it. Also, we stated that the "rule" for quadratic equations is such that when the 'a' term is positive, the curve will be "concave-up". There is yet a third method to determine whether a point is a maximum or minimum value.
If we take the second derivative and if that value is positive, then we are dealing with a minimum value.
In this example, taking the derivative of the derivative we have the value 4 which is positive and so we know this is a minimum.

For equations of the type aX² + bX + c =0, a handy tool to use is the Quadratic Equation Calculator. Not only does this calculate the roots of the equation, it will also show the derivative and the point at which the maximum or minimum exists.

The second example we will look at is very similar to the previous one, except that it is "concave down" instead of "concave up". If you think you understand the concepts presented so far, then move on to Part II

Okay, let's examine this equation: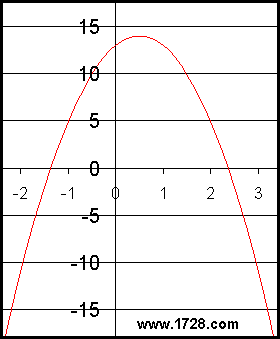

-4X² + 4X + 13 = 0 Since this is a quadratic equation in one variable with the 'a' term being negative, we know that the graph of the curve will be shaped "concave down" (shaped like ∩) and it will have a maximum value but no minimum value (okay, if you want to be technical, its minimum value is negative infinity. You happy now?).

We learned from the first example that the way to calculate a maximum (or minimum) point is to find the point at which an equation's derivative equals zero. The derivative of this equation is: -8X + 4 and when -8X + 4 = 0, then X= .5 and it is at that point where the maximum of the curve is located. As for the 'Y' value, we substitute .5 into the original equation and get: Y = -4*(.5*.5)² +4*.5 + 13 Y = 14 So, at point X=.5, Y= 14 there exists a maximum value.
Taking the second derivative of -8X + 4, we get -8. Since this is negative, it means that we have found a maximum value.

Now it is time to move on to Part II

__________________

Return To Home Page