If you have studied algebra, you are probably familiar with grahping equations by using "x" and "y" values to plot points on a graph. (see illustration). This is known as the Cartesian coordinate method, named after its inventor, the French mathematician René Descartes (1596 - 1650). The horizontal x-axis (the abscissa) and the vertical y-axis (the ordinate) divide the graph into four quadrants. These four quadrants are always represented by Roman numerals and they are numbered, starting with the upper right quadrant going counterclockwise. So, if we were asked in which quadrant is the point (-2,-5) located, we'd say it is in Quadrant III because here, all x and y values are negative. That's about all you need to know about quadrants when studying algebra.

In trigonometry, the above graphic is quite hepful in showing which of the 6 trigonometric functions are either positive or negative in each of the four quandrants. (If the function is printed in blue, it is positive in that quadrant and a red font indicates negative). Another graphic would be helpful in showing this.

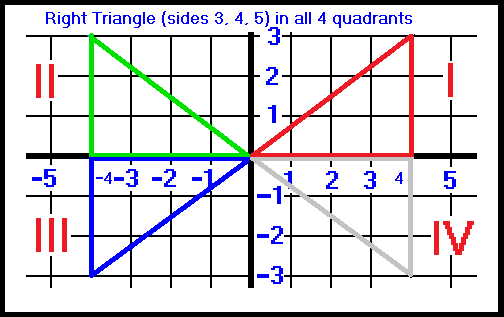
Here, we have drawn a right triangle (with sides 3, 4 and 5) in each of the 4 quadrants. Since all 6 trigonometric functions are positive in the first quadrant , let's look at the green triangle in quadrant II. How can we tell if the sine function is postive or negative in the second quadrant? • The sine function equals the opposite side (y-value) divided by the hypotenuse. As we can see the y-value is positive and so the sine value is positive. • The cosine function equals the adjacent side (x-value) divided by the hypotenuse. The adjacent side is negative and therefore the cosine value is negative. • The tangent function equals the opposite side (y-value) divided by the adjacent side (x-value). Even though the opposite side is positive, the adjacent side is negative and therefore the tangent value is negative. • cotangent function = adjacent side (x-value) ÷ opposite side (y-value). adjacent side is negative, therefore cotangent is negative. • secant function = hypotenuse ÷ adjacent side (x-value). adjacent side is negative, therefore secant is negative. • cosecant function = hypotenuse ÷ opposite side (y-value). opposite side (y-value) is positive therefore cosecant is positive. You can easily determine these for the other quadrants.