This method will calculate the area of a trapezoid, without knowing the trapezoid height and not using the area formula. Let's use this trapezoid as an example.

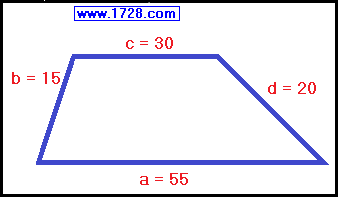
First, we need to calculate the trapezoid height. To do this, we drop perpendiculars (called 'hgt' for height) from the upper base to the lower base, producing the image you see below:

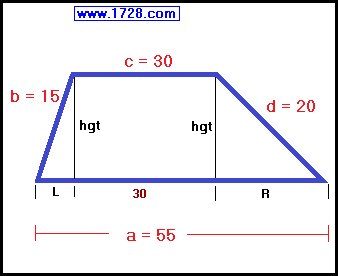
Using the Pythagorean Theorem, we can create two equations for calculating the trapezoid height. hgt2 = 152 -L2   or   hgt2 = 225 -L2 hgt2 = 202 -R2   or   hgt2 = 400 -R2 Since the right side of both equations = hgt2, we can state that both equations equal each other: 225 -L2 = 400 -R2   or a) L2 = R2 -175 We know that L + R + 30 = 55 so, we can create 2 more equations: L = 25 -R   and   R = 25 -L If we square L = 25 -R we get the equation: b) L2 = R2 -50R +625 Since the right side of equations 'a' and 'b' equal L2, we can state that: R2 -175 = R2 -50R +625 50R = 800 R = 16

Now that we have a value of R, we can use the Pythagorean Theorem to calculate the height: hgt2 = 202 -162 Trapezoid height = 12 We know from another equation that L = 25 -R L = 25 -16 L=9 Now, we can calculate the entire area: Triangle Areas = (½*9*12) + (½*16*12) = 54 + 96 = 150 Plus Rectangle Area = 30 * 12 = 360 Trapezoid Area = 510 * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * Calculating Trapezoid Area Knowing Both Bases and height but not knowing the legs and not using the Trapezoid Area Formula This procedure shows how to calculate the area of a trapezoid, knowing both bases and the height and not using the Trapezoid Area Formula and not knowing the length of the trapezoid legs. Using the trapezoid shown, we know the lengths of the short base (c = 30 cm), the long base (a = 55 cm) and the height (hgt = 12 cm) but we do not know the length of both legs (hypotenuse 1 and hypotenuse 2). 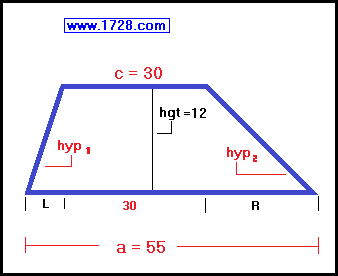Looking at the diagram below, the short base (c) has been extended left and right so that it is exactly the same length as the long base (a). Next, we drop four perpendiculars (b & b' and d & d') from the extended upper base (c) to the lower base (a) and these 4 perpindiculars are the same length as the height (12). 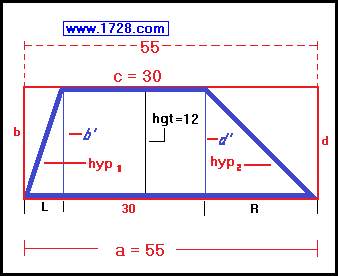The trapezoid now has had a red rectangle (sides a, b, c and d) drawn around it and this rectangle measures: height: 12 cm   width: 55 cm   area: 12 * 55 = 660 cm² We now have a trapezoid that has been extended into a rectangle consisting of 3 smaller rectangles (left, middle and right). The middle rectangle is 12 by 30 cm and has an an area of 360 cm². Determining the area of the remaining 2 rectangles (left and right) is made rather easy by thinking of these as just one rectangle. Since the "middle rectangle" has a length of 30, then the length of the "remaining rectangle" is 55 -30 = 25. It has already been stated that the height is 12 so the total area of the "remaining rectangle" is 25 * 12 = 300 cm². Of course that is more than what the area of the rectangles should be. Looking at the left and right rectangles, we see that the left leg (hypotenuse1) and the right leg (hypotenuse2) precisely bisect both rectangles and so their area should be exactly half of the area we just calculated or 150 cm². So, now we see the total area of the trapezoid is: 360 + 150 = 510 cm²