One of the most famous probability problems (sometimes called the "Birthday Paradox") is calculating how many randomly-chosen people you would need for a 50% chance that at least two have the same birthday.
(We will assume that no one has a February 29th birthday.)
How would we start?

Let's calculate the probability that none of the randomly-chosen people can have the same birthday.

The probability of the first person having any birthday is (365 ÷ 365) which equals 1.

We know that the second person cannot have the same birthday as the first person so we calculate
the probability of the second person having any birthday except the first person's birthday is:
(365 ÷ 365) • (364 ÷ 365) = (132,860 ÷ 133,225) = 0.997260274

The probability of the third person having any birthday except for person 1 or person 2's birthday is:
(365 ÷ 365) • (364 ÷ 365) • (363 ÷ 365) = (48,228,180 ÷ 48,627,125) = 0.9917958341

The probability of the fourth person having any birthday except for person 1, person 2 or person 3's birthday is:
(365 ÷ 365) • (364 ÷ 365) • (363 ÷ 365) • (362 ÷ 365) = (17,458,601,160 ÷ 17,748,900,625) = 0.9836440875

We can carry out these calculations until the probability falls below .5 because we are looking for the probability that none of the chosen people have the same birthday.

As we can see, when we choose 23 people, the probability falls below .5 and here is the actual calculation of that probability: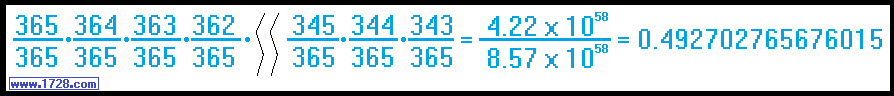

Then, all we have to do is subtract this number from 1 to get the probability that both have the same birthday.
1 –0.492702765676015   =   0.507297234323985

---

To see how accurate this is, let's take a real world example.
There have been 45 people who have been President of the United States.
Even though Joseph Biden is President 46, he is the 45th person because Grover Cleveland gets counted as President 22 and 24.
As it turns out, James Polk and Warren G. Harding were both born on November 2nd.

When it comes to dates of death, the coincidences are more plentiful.
Three Presidents died on July 4th, two died on March 8th and two died on Dec 26th.
Presidential birthdays.

---

To calculate the probability of three or more people having the same birthday, click here.