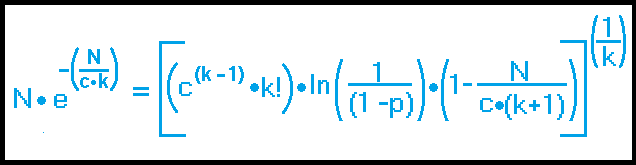Having just calculated this probability for two people, let us now calculate the probability of a 50% chance that three people (chosen from a group of "n" people) will have the same birthday.
(We will assume that no one has a February 29th birthday.)

For calculating this probability, we will need to use this formula:

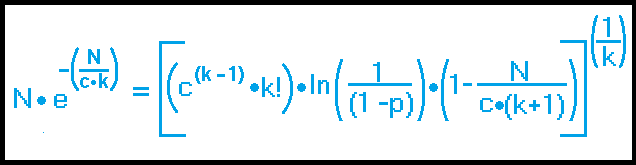
Where:
"k" is the number of coincident birthdays (in this case it is 3)
"c" - the number of days in a year (365)
"e" - the mathematical constant 2.718281828459045...
"p" - the probability (which equals .5 in this case)
"N" - the number of people needed.

Due to the complexity of that formula, it cannot be solved for "N".
To use that formula we employ a trial and error process whereby we keep increasing the values of "N" until the "left side" of that equation becomes greater than the "right side".
To save time, we already calculated the value of "N" (88) and we will only show the actual calculations for "N" = 88.

Filling in the right side of that formula with numbers:

c^{(k -1)} • k!   =   365^{(3 -1)} • 3!   =   133,225 • 6   =   799,350

ln (1 / (1-p))   =   ln (1 / (1 -.5))   =   ln (1 / .5)   =   ln (2)   =   0.6931471806

1 -(N / c • (k + 1))   =   1 -(88 / 365 • (3 + 1))   =   1 -(88 / 1,460))   =   1 -0.0602739726   =   0.9397260274

Then we multiply those 3 numbers 799,350 • 0.6931471806 • 0.9397260274 = 520,671.367621214

And its cube root equals 80.4491077898

Now, let's calculate the left side of the equation.

N • e^{-(N / (c • k))}   =   88 • 2.718281828459045^{-(88 / 365 * 3)}   = 88 • 2.718281828459045^{-(0.0401826484)}   = 88 • 0.9606139685   =

81.2045692937 which completes the left side calculation.

Let us now calculate the "left side" and "right side" values when "N" = 86 and "N" = 87. (To save a lot of time and to minimize errors, the wisest way to make these calculations is to use an electronic spreadsheet such as Microsoft Excel™ or OpenOffice Calc™).

Now let's compare the left side and right side numbers as we vary the values of "N":

"N"     Left Side   Right Side   86   79.504091319     80.4881797278     87   80.3551402886     80.4686485017     88   81.2045692937     80.4491077898   As can be seen, the left side number becomes greater than the right side number when "N" becomes 88. C A L C U L A T O R "N" number of people =   # of coincident birthdays = Equation Left Side =    Equation Right Side = As an example of using this calculator, let's determine how many people we would need to have a 50 per cent chance that four of them would have the same birthday. We know that we need 88 people to get three people with the same birthday so for four, let's take a guess that we'll need 150. We enter 150 for "N" and we enter 4 for the coincident birthdays. Clicking "CALCULATE" we see the left side is lower. So we'll try 170 and show further results in the table below.   "N"     Left Side   150     Low   170     Low   190     High   185     Low   187     High   186     Low So we now know that when "N" = 187, that is the point at which the probability changes to 50%. Here are the calculations worked out for 2 through 13 people.   Coincident   Birthdays     People   Needed   2     23   3     88   4     187   5     313   6     460   7     623   8     798   9     985   10     1,181   11     1,385   12     1,596   13     1,813 Source: Methods For Studying Coincidences (Page 858) Unfortunately, the equation at the top of the page (as well as this calculator) begins to become inaccurate when "N" equals 6 and when "N" equals 13, it calculates 1,809 when it should actually be 1,813. Return To Home Page Copyright © 1999 -     1728 Software Systems