Circle Equations
|
A circle is a two-dimensional shape whose points are all equidistant from the center.
All circles with centers located at the origin (0, 0) have the equation:
x² + y² = r²
Where r is the radius of the circle.
So, a circle whose center is located at the origin (0, 0) with a radius of 4 has the equation:
x² + y² = 16
Standard Form of a Circle's Equation
A circle whose center is located at point (a, b) having a radius of length r has the equation:
(x -a)² + (y -b)² = r²
This is called the standard form of a circle's equation.
(This is sometimes called the center-radius form).
A circle's center coordinates and radius can be easily determined from the standard form.
A circle's center would be found at point (a, b) and its radius equals the square root of r².
So, for example, a circle with the equation (x -2)² + (y -1)² = 25
Would have its center located at (2, 1) and would have a radius equal to the square root of 25 or 5.
A circle with the equation (x +2)² + (y -1)² = 36
Would have its center located at (-2, 1) and would have a radius equal to the square root of 36 or 6.
General Form of a Circle's Equation
Multiplying out a circle's standard form: (x -a)² + (y -b)² = r²
produces the general form of a circle's equation:
x² + y² + cx + dy + e = 0
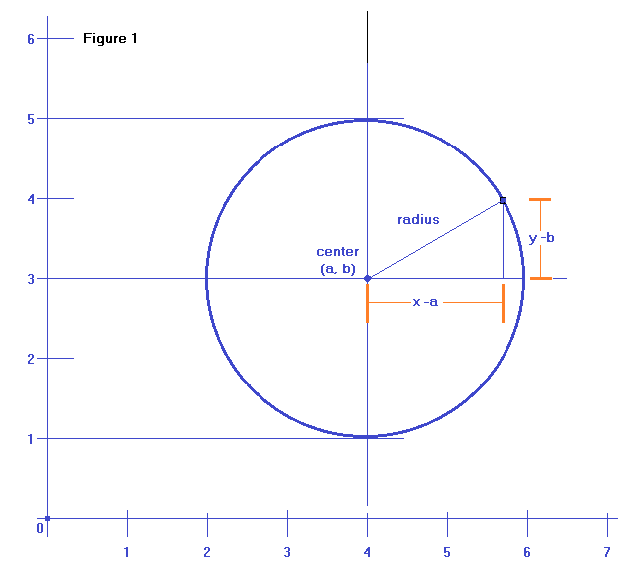
Figure 1 below shows a circle whose center is at point (4, 3) with a radius of 2.
How do we find the standard form equation of this circle?
We put the center coordinates (4, 3) into the a and b variables and we square the radius for r²
(x -4)² + (y -3)² = 4
By multiplying this out, we get the general form
x² -8x + 16 +y² -6y + 9 = 4
x² +y² -8x -6y +21 = 0
Going From General Form To Standard Form
How do you convert a general form equation into a standard form equation?
1) Let's take this general form equation as an example.
x² +y² +16x -18y -145 = 0
2) Set the equation up in this manner and move the "non-x" term to the right.
(x )² + (y )² = 145
3) Looking at the equation in step (1), take the x coefficient (16) and the y coefficient (-18)
divide both these numbers by two, giving us (8, -9)
Insert these numbers into equation 2, paying attention to the signs.
(x + 8)² + (y - 9)² = 145
4) Finally, take the numbers from step 3 (8, -9), square them (64, 81) then add both these numbers to 145, giving us the finished equation:
(x + 8)² + (y - 9)² = 290
A calculator that computes a circle's equation after 3 points have been input is located here.
|
|