D E R A N G E M E N T S Derangements are another type of combination. This time let us choose "1234" as the example. We know these 4 digits can be arranged in 24 ways but to be considered a derangement, the 1 cannot be in the first position, the 2 cannot be in the second position, the 3 cannot be in the third position and the 4 cannot be in the fourth position. Working within these restrictions, and using the "brute force" method, we find there are 9 possible derangements: 2143   2341   2413 3142   3412   3421 4123   4312   4321 Is there an easier way to count derangements? Yes, and the formula is:

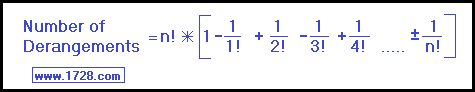
For another method of calculating derangements, click here And the reason for the ± symbol in front of that final term? It depends on whether 'n' is odd or even. If 'n' is odd, then the final term will be (-1 ÷ n!) and if 'n' is even, the final term will be (+1 ÷ n!). Incidentally, derangements (also called subfactorials) are abbreviated with an exclamation mark coming before the number. So, just as we know that 4! equals 24, we now know that !4 = 9. Derangements do have a practical application and here's one good example. Perhaps you have seen math puzzles, with rather odd titles such as "the Inept Secretary", "the Misaddressed Envelopes", "the Drunken Hat Check Girl", "the Drunken Sailor Problem", etc. These puzzles have very similar descriptions and derangements play an interesting role in finding their solution. Let's try solving 1 of these - "the Inept Secretary". A secretary types 'n' letters and then types out 'n' envelopes for those letters. She has not been careful about keeping the letters in the same order as the envelopes. Assuming each envelope gets filled with a randomly-selected letter, what is the probability that all the letters went into an incorrect envelope? 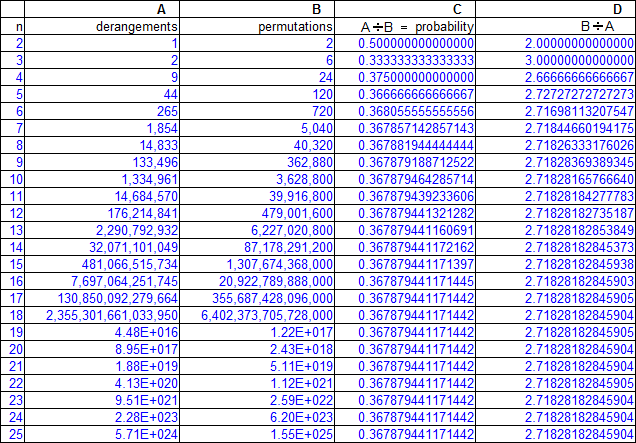The probability of this occurring depends on how many letters ('n') are involved. We calculate all possible outcomes ('n' factorial - column B) and divide that by all instances in which every envelope gets filled incorrectly ('n' derangements - column A). When 'n' = 2 the probability equals .5 and as 'n' increases, the probability converges very quickly on the answer of 0.367879. For another example of this type of puzzle, click on this link, and scroll to puzzle 26. Another Method To Calculate Derangements To calculate the "nth" derangement value, take the (n-1) derangement value and multiply it by n. If "n" is even, add 1. If "n" is odd, subtract 1. That may seem somewhat confusing so let's have an example. How many derangements are there when n = 5? n = 5 when n = 4 (or n-1), there are 9 derangements n • 9   =   5 • 9   =  45 Since n = 5, which is odd, we subtract 1 from 45 and get 44 derangements. Granted, this method requires that you know the previous derangement value. However, if you look at the other formula, this method uses aritmetic calculations that are much more easily manipulated and come in handy if you need to make a table of derangement values. This has nothing to do with the probability problem just presented but column D shows a rather interesting mathematical relationship. If we calculate the number of permutations for a value of 'n' and then divide that by the number of 'n' derangements, the quotient quickly converges on the value of 2.718281828... This particular number is called 'e' and has many interesting uses in mathematics. Click here to read more about it.