|
C a l c u l a t o r I n s t r u c t i o n s
The first two buttons convert Eccentricity to Aspect Ratio and Aspect Ratio to Eccentricity.
For practice, click on the "Eccentricity to Aspect Ratio" button, enter .8, click "Calculate" and your answer will be .6.
NOTE: Eccentricity = Aspect Ratio when it equals 1 ÷ square root (2) (or about .7071)
The remaining five buttons perform much more extensive ellipse calculations. For example, after inputting just two items of data and then
clicking 'CALCULATE', the output boxes will display ellipse perimeter, area, eccentricity, foci distance, Aspect Ratio and much more information.
You can use this calculator for determining the properties of ellipses found in everyday life.
For example, if an elliptical coffee table measures 3.5 feet by 2 feet, click the "Major Axis and Minor Axis"
button, enter the numbers, press "Calculate" and you will see that
perimeter = 8.8008 area = 5.4978 eccentricity = .82065
Yes, information concerning aphelion, perihelion and average distance is also displayed, but if you are not dealing with planetary orbits, you can just ignore these.
This ellipse calculator comes in handy for astronomical calculations.
The asteroid Eros has an orbital eccentricity of .223 and an average distance from the Sun of 1.458 astronomical units.
Click on the "Average Distance and Eccentricity" button, enter these numbers, click "CALCULATE" then you will see its perihelion and aphelion distances along with its perimeter, area, foci distance and so on.
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
It seems in geometry that the ellipse is the "forgotten stepbrother" of the circle even though the ellipse is far more interesting.
First some definitions.
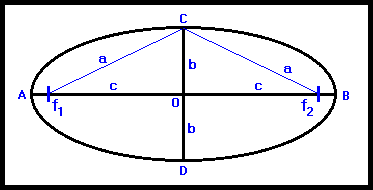 An ellipse
is the locus of points the sum of whose distances
from two fixed points, called foci, is a constant.
An ellipse
is the locus of points the sum of whose distances
from two fixed points, called foci, is a constant.
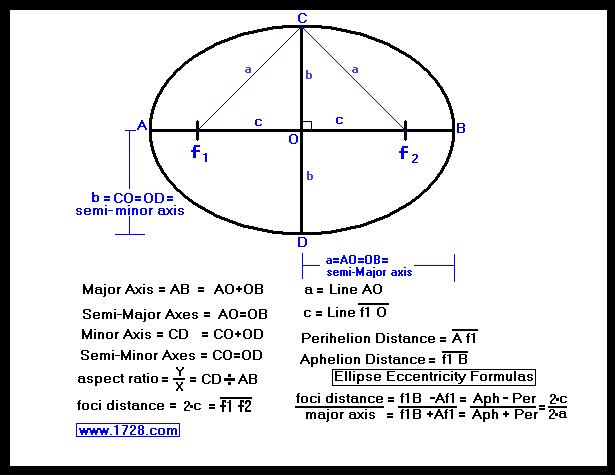
Line AB is the Major Axis (also called Long Axis or Line of Apsides).
Lines AO and OB are the Semi-Major axes which also equals Line a.
Line CD is the Minor Axis and is the perpendicular bisector of the Major Axis.
Lines OC and OD are the Semi-Minor axes which also equals Line b.
Points f1 and f2 are the
foci of the ellipse.
Points A and B are called apses.
Johannes Kepler's First Law states that the planets move in elliptical orbits with the Sun located at one of the foci.
If we were dealing with planetary orbits and we were to say the Sun were at f1 then:
Line A f1 would be the perihelion distance
Line f1 B would be the aphelion distance and
Line AO is the planet's average (or mean) distance and would be one half of the major axis.
For ellipse eccentricity formulas, see the graphic at the top of the page.
As the eccentricity value goes from 0 to 1, the
ellipse goes from circular to highly elongated.
The table below shows the formulas for calculating ellipse perimeter, ellipse aspect ratio and ellipse area.

Surprisingly, unlike the calculation of a circle's perimeter, calculating the cirumference of an ellipse is much more complicated and requires
a rather complex formula. In fact, there is no formula that will precisely generate an ellipse's circumference. The most accurate
equation for an ellipse's circumference was found by Indian mathematician
Srinivasa Ramanujan (1887-1920) (see the above graphic for the formula) and it is this formula that is used in the calculator.
The eccentricity of an ellipse is not such a good indicator
of its shape. For example, Pluto has one of the most
eccentric orbits in the solar system with an eccentricity value of .245. This might
create the impression that the orbit is somewhat flattened. Actually,
by using the calculator, we see that the minor to major axis ratio is
about .97 which is practically circular.
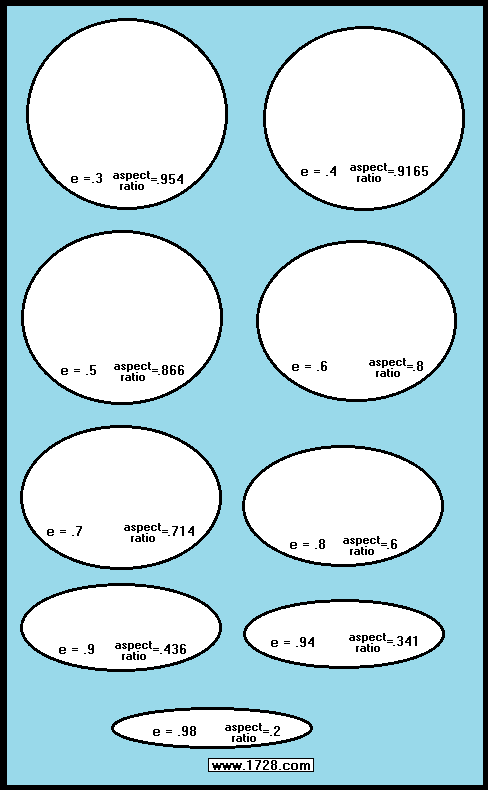
We drew a graphic (see below) to show the shape of an ellipse over a wide range of eccentricities. As you can see, even at an eccentricity of .3 an ellipse still appears as if it is circular, and this is an eccentricity that is even greater than Pluto's.
Drawing Ellipses
The traditional way to draw an ellipse is to make a loop of string or
thread, place two thumbtacks in a sheet of paper, put the loop over the
thumbtacks and then with a pen, keeping the loop tight at all times, go
completely around the thumbtacks.
Referring to the ellipse at the top of the page, the triangle C f1 f2
would represent the loop of string, the thumbtacks would be at f1 and f2
and the pen would start out at point C.
This works fine, except you are not exactly sure of what the ellipse is
going to look like (how eccentric, minor to major axis ratio, etc.).
Therefore this calculator will determine how far apart the thumbtacks have
to be for a required eccentricity.
Example: If you make a loop of string 10 inches long, and want an
ellipse with an eccentricity of .5, enter these figures in the calculator
and your answer will be a thumbtack distance of 6.66666 inches.
Other Ellipse Properties
Referring to the ellipse diagram at the top of the page, let us suppose
that it is a pool table and imagine that f1 and f2 are spots on the table.
If you were to shoot the ball from anyplace over
spot f1, the ball would then go over spot f2, then f1 and so on.
If you
shot the ball through line Af1, the ball would go through line f2B and
no matter how many times it is deflected, the ball will never cross
line f1f2.
Conversely, if you were to shoot the ball anywhere through
f1f2, it will continue to cross line f1f2 with each deflection and will
never travel through Lines Af1 or f2B.
If we were talking about rays of light and the inside of the ellipse were
reflective, the same behavior would be exhibited by the light, just as in the
pool table example.
You may have heard of "whispering galleries" in which one person stands
in a certain spot and whispers while another person stands at another spot
and can hear the other person perfectly. How does this work? The gallery
walls are elliptical in shape, and so if one person stands at f1, the sound
waves will be directed through f2, where the other person will be standing.
One of the chambers in the US House of Representatives is shaped this way.
This web page has only explored the tip of the "ellipse iceberg" so to speak.
For example, the ellipse can also be defined as the locus of points whose
distance ratio from one focus to a straight line (called a directrix) is
equal to the eccentricity of the ellipse. But you probably knew that right?
Also, we barely discussed the mathematical properties of the ellipse such
as ellipse equations. Nor did we discuss the fact that the ellipse is
one of the four conic sections. (See? the fun never ends.)
To find out more about ellipses, use your favorite search engine. No
doubt you will find loads of information. Good luck with your
elliptical internet explorations.
The default setting is for 5 significant figures but you can change that
by inputting another number in the box above.
Answers are displayed in scientific notation and for easier readability, numbers between
.001 and 1,000 will be displayed in standard format (with the same number of
significant figures.)
The answers should display properly but there are a few browsers that will show
no output whatsoever. If so, enter a zero
in the box above. This eliminates all formatting but it is better than seeing no
output at all.
|