EXPONENTIAL GROWTH CALCULATOR

Exponential Growth
Tutorial & Calculator
Based on natural logs and the exponent "e".
To see exponential growth based on common logs and base 10 exponents, click here.
To read about exponential decay particularly half-life, click here.

The abbreviations in the above above formulas stand for:

e = the mathematical constant 2.71828182845904523...
a = beginning amount
y(t) = ending amount
k = rate
t = time

This calculator can solve exponential growth problems whenever three of the four variables a, y(t), k, t are known:
Using the calculator is quite simple:
• Click the variable for which you are solving.
• Enter the appropriate numbers in the 3 input boxes
• Click "CALCULATE" for the answer

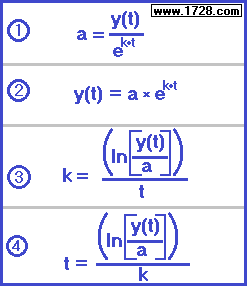
There are four exponential growth problems further down this page.

Do you want to solve for:

1) After 4 hours, a bacteria culture with a growth rate of 20% per hour has grown to a population of 80,000.
What was the bacteria population at the beginning of the experiment (four hours ago.)?

a = y(t) ÷ e^(k•t)

a = 80,000 ÷ 2.71828...^{(.2 • 4)}

a = 80,000 ÷ 2.71828...^(.8)

a = 80,000 ÷ 2.22554

Beginning Amount = 35,946

* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *

2) In 2011, Canada's population was 33,476,688 and was increasing by a rate of 0.016118877 per year.
What will be its population in 2016?

y(t) = a × e ^k*t

y(t) = 33,476,688 × 2.71828... ^{(.016118877 * 5)}

y(t) = 33,476,688 × 2.71828... ^{(0.080594385)}

y(t) = 33,476,688 × 1.0839311486

36,286,425

* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *

3) You have a bank account which doubles your money every 8 years.
What is the interest rate of this account?
For the purpose of solving this problem we'll say that:
a=100 y(t)=200

k = (ln [y(t) ÷ a]) ÷ t

k = (ln [200 ÷ 100]) ÷ 8

k = (ln [2]) ÷ 8

k = (0.6931471806) ÷ 8

k = 0.0866433976

k = 8.66433976%

* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *

4) A bacteria culture begins with a population of 2,500 and increases to 3,000 after 2 hours.
How long will it take the population to triple? (That is, when will the population be 7,500?)

We first must solve for the rate.
k = (ln [y(t) ÷ a]) ÷ t

k = (ln [3,000 ÷ 2,500]) ÷ 2

k = (ln [1.2]) ÷ 2

k = ( 0.182321556793955 ) ÷ 2

k = 0.0911607783969773

Now, we can solve for the time.

t = (ln [y(t) ÷ a]) ÷ k

t = (ln [7,500 ÷ 2,500]) ÷ 0.0911607783969773

t = (ln [3]) ÷ 0.0911607783969773

t = (1.09861228866811) ÷ 0.0911607783969773

t = 12.0513702053 hours

If we were to solve this problem using the calculator, we would first click the rate function, enter the numbers, and then use this rate calculation after we click the time function.

The default setting is for 5 significant figures but you can change that by inputting another number in the box above.

Answers are displayed in scientific notation and for easier readability, numbers between .001 and 1,000 will be displayed in standard format (with the same number of significant figures.)
The answers should display properly but there are a few browsers that will show no output whatsoever. If so, enter a zero in the box above. This eliminates all formatting but it is better than seeing no output at all.

Return To Home Page