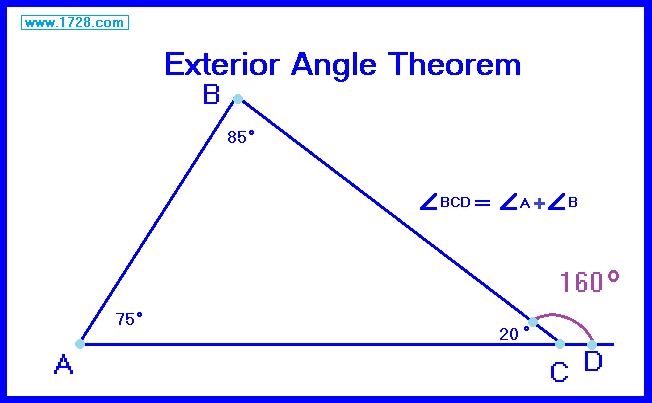This states that any exterior angle (∠BCD) of a triangle equals the sum of both interior angles (∠A) and (∠B) at the other 2 triangle vertices.

This is very easy to prove.
The sum of all 3 angles in a triangle always equals 180°.  A straight angle always equals 180°.
Notice that angle ACB is common to both △ ABC and the straight angle (line ACD. So by eliminating angle ACB (20°) from the triangle and the straight angle, we see exterior angle C (160°) equals interior angle A (75°) plus interior angle B (85°).

Alternate Exterior Angles Theorem

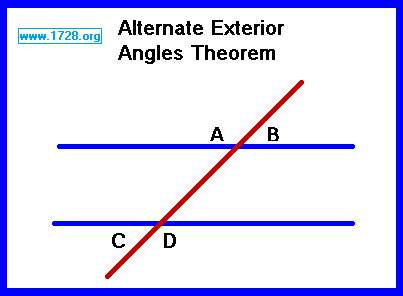
This states that when 2 parallel lines (the blue lines) are intersected by a transversal (the red line), then the alternate exterior angles are equal. That is ∠ A = ∠ D and ∠ B = ∠ C.