HALF-LIFE CALCULATOR

Half-Life Calculator
If you want to see the more traditional equations that involve calculating λ (lambda), then click here.
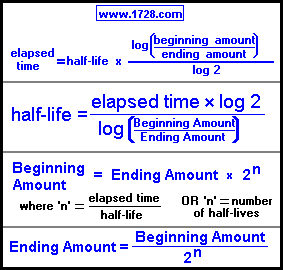
However, if you are just here to use the calculator then stay on this page.

The above formulas are used in calculations involving the exponential decay of radioactive materials.
This calculator can solve half life problems whenever three of the four variables are known:
• time
• half life
• beginning amount
• ending amount

There are four half life problems further down this page.

Do you want to solve for:

or or or

>>>>>
>>>>>
>>>>>

1) You start with 100 grams of sulfur-35, which has a half life of 87.51 days. How much time will it take until only 10 grams remain?
elapsed time = half life * log (beginning amount / ending amount) / log 2
elapsed time = 87.51 * (log (100 / 10) / .30103)
elapsed time = 87.51 * (1 / .30103)
elapsed time = 290.70 days

2) You measure the radioactivity of a substance, then when measuring it 120 days later, you find that it only has 54.821 % of the radioactivity it had when you first measured it. What is the half life of that substance?

Half life = (time * log 2) / log (beginning amount / ending amount)
Half life = (120 * .30103) / log (1 / .54821)
Half life = 36.1236 / log (1.8241)
Half life = 36.1236 / .26105
Half life = 138.38 days

3) Your professor tells you to measure a sample of phosphorus-32 (half life = 14.263 days). You forget about this until 7 days later, you measure its mass to be 37 grams.
(Luckily, in that intervening week, the sample was safely isolated and all safety rules and regulations regarding the proper handling of radioactive materials were strictly enforced.)
What was the mass of phosphorus-32 one week before, when you were supposed to measure it?

Beginning amount = ending amount * 2 ^{(time / half-life)}
Beginning amount = 37 * 2^{(7 / 14.263)}
Beginning amount = 37 * 2^(.49078)
Beginning amount = 37 * 1.4052
Beginning amount = 51.993 grams

4) Hydrogen-3 or tritium as it is commonly called, has a half life of 12.32 years. If you start with 20 grams of it, how much will remain after 25 years?

Ending Amount = Beginning Amount / 2^{(time / half-life)}
Ending Amount = 20 / 2^{(25 / 12.32)}
Ending Amount = 20 / 2^(2.0292)
Ending Amount = 20 / 4.0818
Ending Amount = 4.8997 grams

Significant Figures >>>
The default setting is for 5 significant figures but you can change that by inputting another number in the box above.

Answers are displayed in scientific notation and for easier readability, numbers between .001 and 1,000 will be displayed in standard format (with the same number of significant figures.)
The answers should display properly but there are a few browsers that will show no output whatsoever. If so, enter a zero in the box above. This eliminates all formatting but it is better than seeing no output at all.

Return To Home Page
Copyright © 1999 - 1728 Software Systems