Calculus - Calculating Minimum and Maximum Values

Calculus - Calculating
Minimum & Maximum Values
Part II

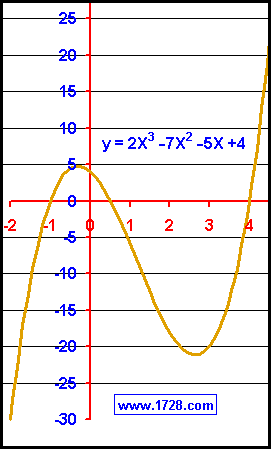
This is a graph of the equation 2X³ -7X² -5X +4 = 0.
Now we are dealing with cubic equations instead of quadratics.
From Part I we know that to find minimums and maximums, we determine where the equation's derivative equals zero.
The equation's derivative is 6X² -14X -5

and when this derivative equals zero 6X² -14X -5 = 0

the roots of the derivative are 2.648 and -.3147

Notice we have 2 extreme points, whereas in Part I, we only had one.
Now we determine whether we are dealing with a maximum or a minimum. Taking the second derivative we get:

12X -14 In Part I, second derivatives only had numbers. Now we have numbers and an 'X' term to deal with. This is no problem though.
Inputting 2.648 into the second derivative we get 17.776 which is greater than zero so we have a minimum at that point.
When X= -.3147, the second derivative value is -17.776 and being less than zero we have a maximum.
Of course if you look at the graph, you can see that the left side of the graph starts from negative infinity, and the right side goes on to infinity. So, in this case we are talking about a relative maximum at point X = -.3147 and a relative minimum at point X= 2.648.
To obtain the 'Y' values, we input 2.648 and -.3147 into the original equation 2X³ -7X² -5X +4 = 0 , and we get values of -21.188 and 4.818 respectively.

So, the relative minimum is at (X= 2.648, Y= -21.188)
and the relative maximum is at (X= -.3147, Y= 4.818)

Click here to go to Part III

__________________

Return To Home Page