Newton's Method

Sometimes you may encounter an equation such as X³ = 70, which is not immediately solvable. There is a branch of mathematics called numeric analysis which is specifically concerned with the solution of these equations, sometimes referred to as implicit equations or implicit functions. One of the procedures for solving such an equation is known as the Newton-Raphson Method, developed by British mathematicians Isaac Newton (1642-1727) and Joseph Raphson (1648-1715).

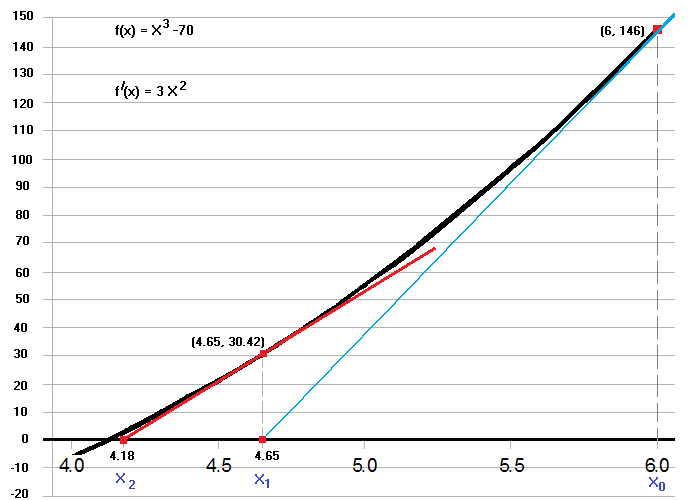Showing Newton's Method Graphically Demonstrating Newton's Method by using graphs and mechanical calculations is the best way to illustrate the way it works.
If you just want to know how to use the formulas, then skip this section.

We will solve for x in the function x³ -70 = 0.
First, we take a guess (called x₀) as to what the value of x might be. This doesn't even have to be a very good guess, so let's say that x₀ = 6.

Solving for X₁ Next, using a theorem from linear approximations, a more accurate solution x₁ can be obtained by taking the slope at the point f(x₀, y) then drawing a tangent line through this point and extending it so that it intersects the x axis at x₁.

To determine the slope at f(x₀, y) we take the derivative of f(x) = X³ - 70 which is 3X² then we input 6 (the value of x₀) into the derivative, yielding a slope value of 108.
When x = 6 the y value calculates to 146.
With these two pieces of information, we can calculate the value of x₁.
The slope value of 108 means that every time the y value decreases by 108, the x value decreases by one.
At point x₁ since the y value decreases from 146 to 0, the x value decreases by 146 ÷ 108 (or about 1.35185185...) which makes x₁ equal to 6 minus 1.35185185... or 4.648148148...
(In the diagram above, note the blue line intersecting the x axis at x₁).

Solving for X₂ By repeating the steps we just used to get the value of X₁, we can now calculate the slope of the red tangent line, the value of y at f(4.648..., y) and the value of X₂.

Once again we'll use the derivative of f(x), 3X², insert x₁ = 4.648... and obtain the red line's slope value of 64.8158...
Putting x₁ = 4.648... into the equation f(x) = X³ -70, yields a y value of 30.424...
Again, we have generated two pieces of information, by which we can calculate the value of x₂.
The slope value of 64.8158... means that every time the y value decreases by 64.8158..., the x value decreases by one.
At point x₂ since the y value decreases from 64.8158... to 0, the x value decreases by 30.424... ÷ 64.8158... (or about .46939...) which yields a value of x₂ = 4.648... minus .46939 which equals 4.1787...
(See the red line in the diagram).

As you can see, Newton's method converges on an answer quite rapidly but the graph is too crowded to show the answer for X₃ so we will do this in the next section.

Newton's Method Using Formulas

We'll solve f(x) = X³ - 70 using just the formula.
(You'll need to know the derivative of X³ - 70 which is 3X²)
The formula works in the following way.
To get the next value of X, we
• get the previous value of X and
• subtract from it the fraction f(x) ÷ f '(x)
(using the previous value of X in the fraction as well)

This is much easier to see in actual calculations.

We'll make an initial guess of X₀ = 6.
X₁ = 6 - (6³ -70) / (3 • 6²)
X₁ = 6 - (146 / 108)
X₁ = 6 - 1.3518518519
X₁ = 4.648148148...

X₂ = 4.648148148... - (4.648148148³ -70) / (3 • 4.648148148²)
X₂ = 4.648148148... - (30.424547833) / (64.8158436214)
X₂ = 4.648148148... - 0.4693998586
X₂ = 4.178748289...

If you want to scroll up to the first section, you can see how these numbers were generated without using the formula.

Solving for X₃
X₃ = 4.17874828... - (4.17874828³ -70) / (3 • 4.17874828²)
X₃ = 4.17874828... - (2.9690399882) / (52.3858115628)
X₃ = 4.17874828... - 0.0566764148
X₃ = 4.12207186...
Using logarithms we can get a very precise answer of 4.12128529980856 for the solution of the equation X³ - 70 = 0 but as you can see, just using 3 steps of Newton's method and making an inaccurate first guess, we have an answer of 4.122. (accurate to about .025%)

We'll continue with these X calculations, (without showing all the steps) to get these values:
X₄ = 4.12128544988990
X₅ = 4.12128529980856
X₆ = 4.12128529980856
By comparing X₆ to X₅ we can see that after using Newton's Method for just five steps, we have an answer that is accurate to 14 decimal places. Despite this rather rapid convergence to an answer, don't think that Newton's Method converges this quickly every time you use it. Also remember that this method does not give you "the" answer. Instead it generates increasingly more accurate values of 'x' and you have to decide how much accuracy you need.

A Real World Example

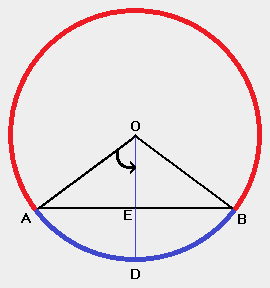
The arc length (curved blue line ADB) of a circle is 16 and its chord length (line AB) is 14. (Therefore arc AD = 8 and line AE = 7)
How can we solve for the other parts of the circle?
We can see from the graphic of the circle that:

Since both equations equal the radius AO, we then can say:

Rather than deal with two numbers, we'll let the letter 'n' equal the ratio of AE ÷ (arc AD).

Putting the equation in standard form we have:

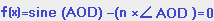
Angle AOD can't be isolated because this is an implicit equation and requires Newton's Method to solve it.

We will need the derivative of f(x) which is:
f '(x) = cos ∠ AOD -n = 0
The value of n = (Chord AB / Arc AB) = (14 / 16) = .875

To start, let's guess that X₀ (or angle AOD) is 1 radian.
X₁ = X₀ - [ f(X₀) ÷ f'(X₀) ]
X₁ = 1 - [ {(sin(1) -(n * 1)} / (cos(1) -n) ]
X₁ = 1 - [ {0.8414709848 -(.875*1)} / (0.54030230587 -.875) ]
X₁ = 1 - [ -0.03352901519 / -0.33469769413 ]
X₁ = 0.8998229872

X₂ = X₁ - [ sin(X₁) -(n * X₁) / cos(X₁) -n ]
X₂ = 0.8998229872 - [ {sin(0.8998229872) -(.875 * 0.8998229872)} / (cos(0.8998229872) -.875) ]
X₂ = 0.8998229872 - [ {0.7832168644 -0.7873451138} / (0.6217486174 -.875) ]
X₂ = 0.8998229872 - [ -0.00412824936 / -0.25325138258 ]
X₂ = 0.8835219928

X₃ = X₂ - [ sin(X₂) -(n * X₂) / cos(X₂) -n ]
X₃ = 0.8835219928 - [ {sin(0.8835219928) -(.875 * 0.8835219928)} / (cos(0.8835219928) -.875) ]
X₃ = 0.8835219928 - [ (0.7729781357 -0.77308174371) / (0.6344326613 -.875) ]
X₃ = 0.8835219928 - [ -0.00010360801 / -0.2405673387 ]
X₃ = 0.8830913110

If we were to compute a value for X₄ it would equal 0.8830910126, which shows that X₃ is accurate to six decimal places which is adequate for most practical applications.
So, now that we have determined that angle AOD equals .883091 radians ( or 50.5974 degrees), we can calculate the remaining parts of the circle.

The central angle AOB equals 2 * 50.5974 or 101.195 degrees.

The radius = line AE / sin(AOD)
radius = 7 / sin (50.5974)
radius = 9.0591
Now that we have this information, the rest of the circle can be easily solved.

Return To Circle Calculator

Return To Home Page