|
These 5 geometric figures are also known as the 5 Platonic Solids and are the only convex regular polyhedra that can exist.
A regular polyhedron is defined as a solid three-dimensional object having faces where
• each face is a regular polygon. (A regular polygon has equal sides and equal angles).
• the same number of faces (or the same number of edges) meet at each vertex
• all the dihedral angles (the angles between the planes) are equal
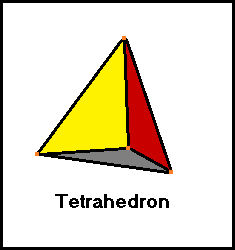
3 faces and 3 edges meet at each vertex
Each face is an equilateral triangle.
4 faces
4 vertices
6 edges
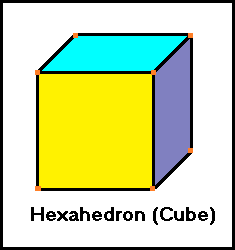
3 faces and 3 edges meet at each vertex
Each face is a square.
6 faces
8 vertices
12 edges
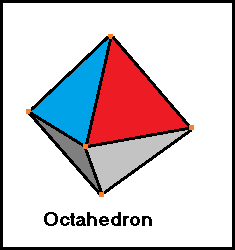
4 faces and 4 edges meet at each vertex
Each face is an equilateral triangle.
8 faces
6 vertices
12 edges
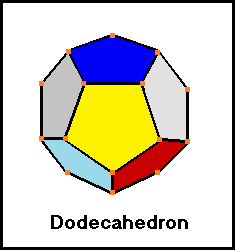
3 faces and 3 edges meet at each vertex
Each face is a pentagon.
12 faces
20 vertices
30 edges
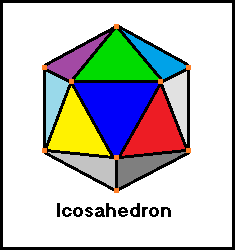
5 faces and 5 edges meet at each vertex
Each face is an equilateral triangle.
20 faces
12 vertices
30 edges
The Swiss mathematician Leonhard Euler (1707-1783) discovered the formula
V -E +F = 2 which states that the vertices minus the edges plus the faces of a convex polyhedron will always equal two.
If we were to inscribe a sphere within any of the 5 Platonic solids, it would be tangent to the center of each face.
If we were to circumscribe a sphere outside any of the 5 Platonic solids, it would pass through all of the vertices.
C A L C U L A T O R
P O L Y H E D R A F O R M U L A S

The default setting is for 5 significant figures but you can change that
by inputting another number in the box above.
Answers are displayed in scientific notation and for easier readability, numbers between
.001 and 1,000 will be displayed in standard format (with the same number of
significant figures.)
The answers should display properly but there are a few browsers that will show
no output whatsoever. If so, enter a zero
in the box above. This eliminates all formatting but it is better than seeing no
output at all.
Return To Home Page
Copyright © 1999 -
1728 Software Systems
|