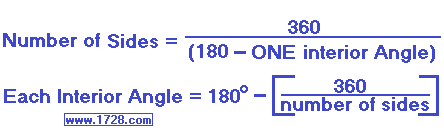|
Regular Polygon Calculator
Scroll down for Instructions and Definitions
To see a listing of the 22 polygons that have integer angles, click here.
Regular Polygons
This calculator works only for regular polygons -
those polygons which have ALL sides equal & ALL interior
angles equal.
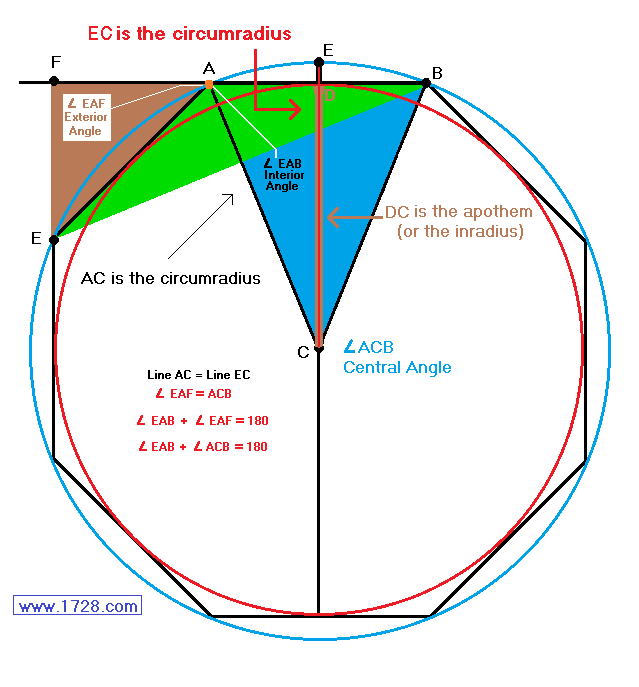
The figure below shows a regular octagon.
The outer circle surrounding it is called a circumscribed circle (or circumcircle)
and the inner circle which is surrounded by the octagon is called the
inscribed circle (or incircle).
Angle EAB is one of the 8 interior angles.
Angle EAF is one of the 8 exterior angles and
equals central angle ACB.
Line AC (which also equals Line EC) is called the circumradius (the radius of the outer,
circumscribed circle).
Line DC is called the inradius or the apothem (the radius of the inscribed circle).
To see a list of the 22 polygons that have integer angles, click here.
Input data in the first 2 boxes on the right, then click 'Calculate'.
Sum of Interior Angles = (Number of Sides -2) • 180 degrees
Number of Sides = (Sum of Interior Angles ÷ 180) + 2
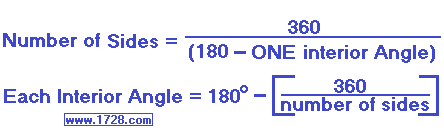
Each Exterior Angle = Each Central Angle = (360 degrees) ÷ (Number of Sides)

Polygon Names
| Sides | Name | Sides | Name | Sides | Name |
| 3 | triangle | 9 | nonagon | 15 | pentadecagon |
| 4 | quadrilateral | 10 | decagon | 16 | hexadecagon |
| 5 | pentagon | 11 | hendecagon | 17 | heptadecagon |
| 6 | hexagon | 12 | dodecagon | 18 | octadecagon |
| 7 | heptagon | 13 | tridecagon | 19 | enneadecagon |
| 8 | octagon | 14 | tetradecagon | 20 | icosagon |
The default setting is for 5 significant figures but you can change that
by inputting another number in the box above.
Answers are displayed in scientific notation and for easier readability, numbers between
.001 and 1,000 will be displayed in standard format (with the same number of
significant figures.)
The answers should display properly but there are a few browsers that will show
no output whatsoever. If so, enter a zero
in the box above. This eliminates all formatting but it is better than seeing no
output at all.
Return To Geometry Index
Return To Home Page
Copyright © 1999 -
1728 Software Systems
|