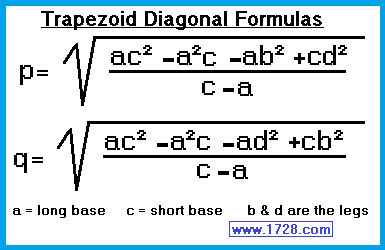
|
* * * * * * * * * E x a m p l e * * * * * * * * *
A trapezoid has bases that are 30 and 55 centimeters in length and the non-parallel sides (or legs) are 15 and 20 centimeters.
What is the area of the trapezoid?
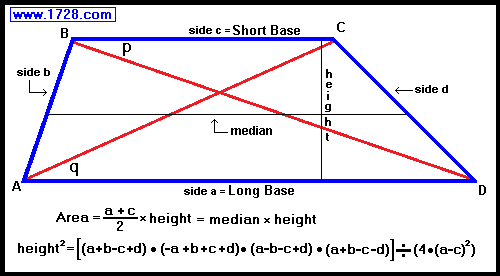
Going by the diagram, we shall label the 4 sides as:
a = 55 b = 15 c = 30 d = 20
Before we can use the area formula, we first have to determine the height of the trapezoid.
(height)2 = (a+b-c+d) • (-a+b+c+d) • (a-b-c+d) • (a+b-c-d) ÷ (4 • (a -c)2)
(height)2 = (55+15-30+20) • (-55+15+30+20) • (55-15-30+20) • (55+15-30-20) ÷ (4 • (55 -30)2)
(height)2 = (60) • (10) • (30) • (20) ÷ (4 • (25)2)
(height)2 = 360,000 ÷ 2,500
(height)2 = 144
height = 12 cm
Now to use the area formula:
trapezoid area = ((sum of the bases) ÷ 2) • height
trapezoid area = ((55 + 30) ÷ 2) • 12
trapezoid area = 510 cm²
To see how to calculate trapezoid area without using formulas, click here.
* * * * * * * * * Trapezoids * * * * * * * * *
ALL TRAPEZOIDS have the following
properties:
1) ONE pair of opposite sides are parallel.
(BC and AD)
2) The sum of the angles attached to the same leg = 180°
∠ 'A' plus ∠ 'B' = 180°
∠ 'C' plus ∠ 'D' = 180°
4 special cases of trapezoids are worth mentioning.
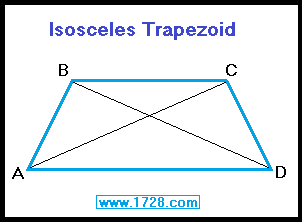 
The isosceles trapezoid has
both legs of equal length. AB = CD
Both diagonals are equal. AC = BD
Lower base angles are equal. ∠ A = ∠ D
Upper base angles are equal. ∠ B = ∠ C
Angles attached to the same leg are supplementary. ∠ A + ∠ B = 180° ∠ C + ∠ D = 180°
Opposite angles are supplementary. ∠ A + ∠ C = 180° ∠ B + ∠ D = 180°
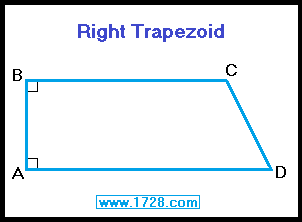
The right trapezoid has
two right angles.
A trapezoid cannot have just one right angle because this prevents any sides from being parallel.
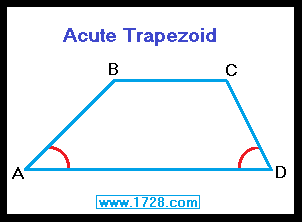 
The acute trapezoid has two acute angles (A & D) located on each side of the long base (Line AD) and
it has two obtuse angles (B & C) on each side of the short base (Line BC).
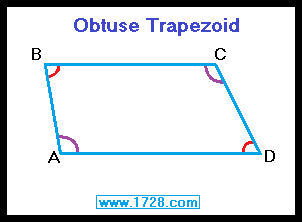
The obtuse trapezoid has two obtuse opposite angles (A & C) and two acute opposite angles (B & D)
OR (using the same graphic)
it has one acute angle and one obtuse angle on each base: angles (B & C) and angles (A & D)
The default setting is for 5 significant figures but you can change that
by inputting another number in the box above.
Answers are displayed in scientific notation and for easier readability, numbers between
.001 and 1,000 will be displayed in standard format (with the same number of
significant figures.)
The answers should display properly but there are a few browsers that will show
no output whatsoever. If so, enter a zero
in the box above. This eliminates all formatting but it is better than seeing no
output at all.
Return To Geometry Index
_____________________
Return To Home Page
Copyright © 1999 -
1728 Software Systems
|