Surprisingly, you can calculate all three triangle heights and all three angles with what you already know.
For example, let's calculate triangle altitude ha using this triangle.
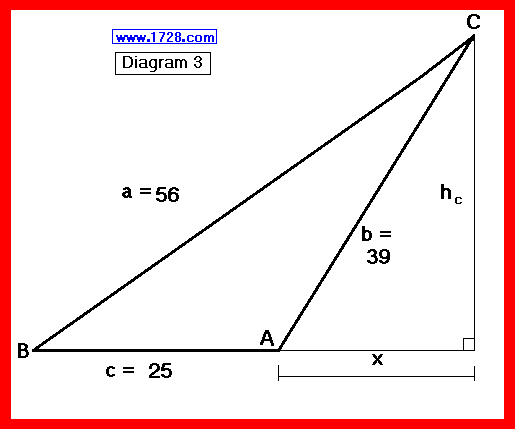
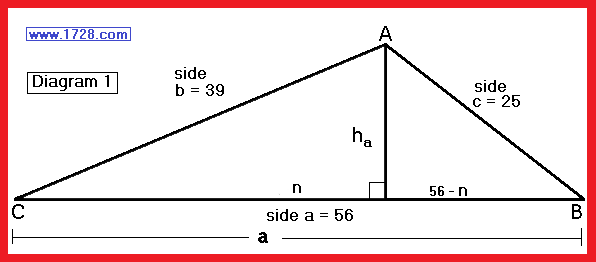First, we drop perpendicular "ha" from vertex A to side "a" which splits side "a" into "n" and "56-n".
From the Pythagorean Theorem, we know that (ha)² = 39² - n² giving us equation A)
A) ha² = 1,521 - n²
and we know that
ha² = 25² - (56 -n)²
ha² = 625 - (3,136 -112n +n²)
giving us equation B)
B) ha² = -2,511 +112n -n²
Looking above, we have 2 equations equal to ha² so we'll make those equations equal to each other:
1,521 - n² = -2,511 +112n -n²
4,032 = 112n
n = 36 which means that 56 -n equals 20
We now have enough information to solve for all 3 angles.
The cosine of ∠C = 36 / 39 = 0.9230769231
∠C = 22.62 Degrees
The cosine of ∠B = 20 / 25 = .8
∠B = 36.87 Degrees
Since all triangles have 3 angles that always sum to 180° we can easily calculate the third angle from this equation:
∠A = 180° -22.62° -36.87°
∠A = 120.51°
* * * * * * * * * * * * * * * * * * * * * * * * *
We've just seen the calculation of one altitude and all three angles of a triangle, using mathematics with which we are already familiar.
From this point, we will show how to solve for triangle altitudes and angles by using these three formulas:.
  
Let's take a look at the triangle we just analyzed, in order to calculate a second altitude.
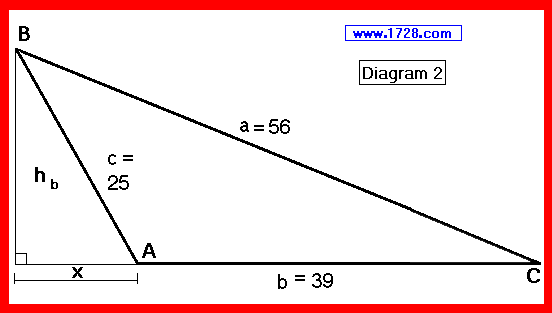
Diagram 2 looks very different from Diagram 1, but those triangles are congruent. The only difference being that the image was rotated about 180° to show the altitude hb more clearly.
The rule for drawing triangle altitudes is that they are drawn from a triangle's vertex (B) perpendicularly to the side (b) that the angle intersects. In this case, the triangle side b had to be extended so that it would intersect with hb
An obtuse triangle, like all triangles, has 3 altitudes (heights). However, with an obtuse triangle, two of the three
altitudes lie outside of the triangle!!! (see diagrams 2 and 3)
Now, let's do some calculations with the equations we just posted.
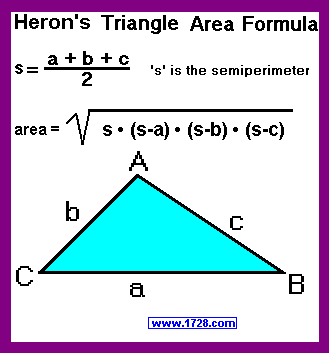
Let's start with calculating the triangle's semiperimeter which equals one half of the sum of the sides divided by 2:
Semiperimeter = (56 + 39 + 25) ÷ 2 = 60
Now we'll calculate the area using Heron's Formula:
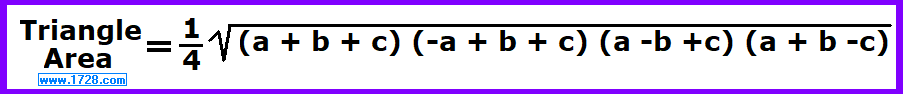
Area = Square Root [ 60 * (60 -56) * (60 -39) * (60 -25) ]
Area = Square Root ( 60 * 4 * 21 * 35 )
Area = 420
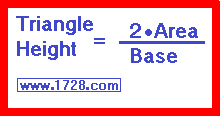
Calculating the triangle heights.
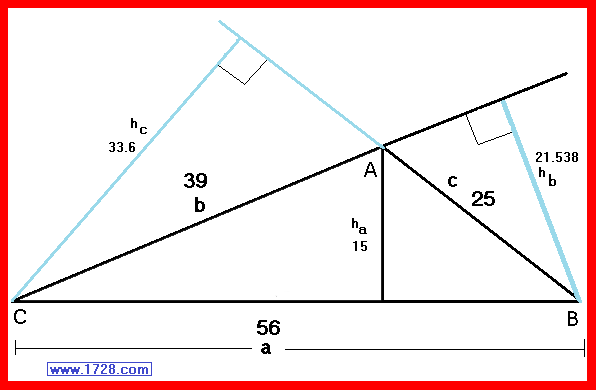
ha = 2 * Area ÷ Base a = 2 * 420 ÷ 56 = 15
hb = 2 * Area ÷ Base b = 2 * 420 ÷ 39 = 21.53846
hc = 2 * Area ÷ Base c = 2 * 420 ÷ 25 = 33.6
Calculating all 3 angles using the Law of Cosines.
arc cos (A) = (b² + c² - a²) ÷ (2 * b * c) = [(1,521 + 625 -3,136)] ÷ [(2 * 39 * 25)] = -990 ÷ 1,950 = -0.5076923 = 120.51°
arc cos (B) = (a² + c² - b²) ÷ (2 * a * c) = [(3,136 + 625 - 1,521)] ÷ [(2 * 56 * 25)] = 2,240 ÷ 2,800 = .8 = 36.87°
arc cos (C) = (a² + b² - c²) ÷ (2 * a * b) = (3,136 + 1,521 - 625 ) ÷ (2 * 56 * 39) = 4,032 ÷ 4,368 = 0.9230769 = 22.62°
And just to complete this discussion, here is the third graphic of ∆ ABC with the altitude hc drawn.
And as a final graphic, here is the triangle with all 3 altitudes drawn, and all side lengths and altitude lengths listed.
The default numeric display is 5 significant figures.
Numbers > -1,000 and <1,000 are NOT in scientific notation.
You can change the display option by changing the number in the box above.
Entering a zero eliminates all formatting.
Return To Home Page
Copyright © 1999 -
1728 Software Systems
|