Triangle Centers

There are literally many triangle centers, but we will just discuss four:
1) incenter 2) circumcenter 3) centroid and 4) orthocenter.

Incenter

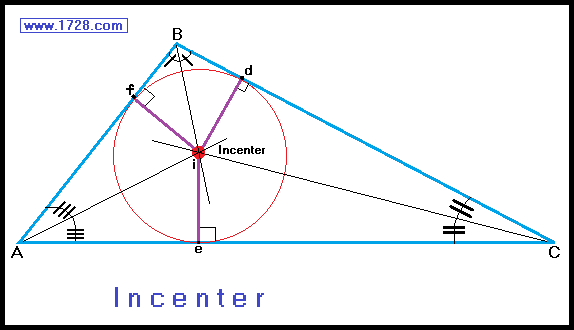
If we were to draw the angle bisectors of a triangle they would all meet at a point called the incenter.
The incenter is always inside the triangle whether it is acute, right or obtuse.
The incenter is equidistant from all three triangle sides. (That is to say the three distances id, ie and if are equal).
If we wanted to inscribe a circle within a triangle, the center of that circle would be the incenter.

Circumcenter

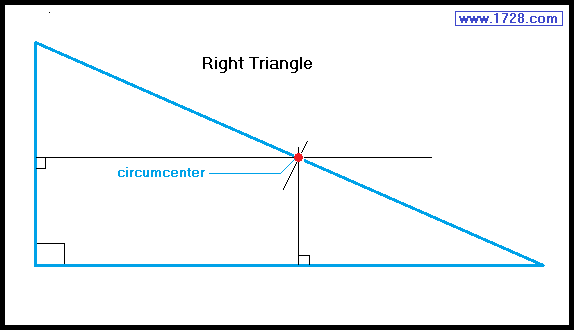
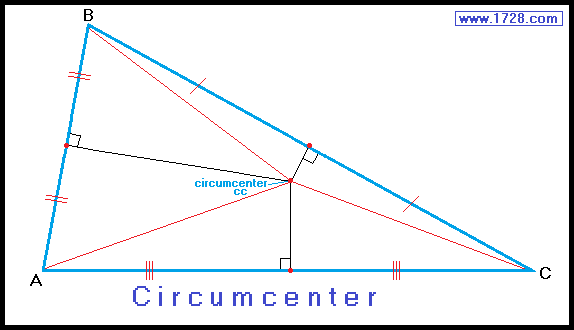The circumcenter is the meeting point of the 3 perpendicular bisectors of a triangle's sides.
It is also the point that is equidistant from all 3 vertices (line A cc = line B cc = line C cc).

The circumcenter is the center of a circle that is circumscscribed about a triangle with the circle passing through all three vertices.

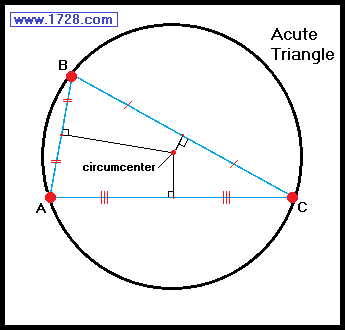
The circumcenter of an acute triangle is always inside the triangle.
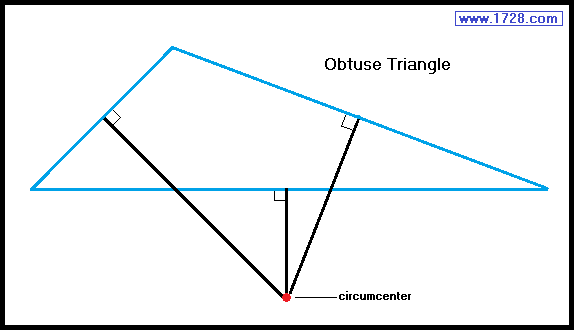
The circumcenter of an obtuse triangle is always outside of the triangle and opposite the obtuse angle.
In a right triangle, the circumcenter lies on the midpoint of the hypotenuse.

Centroid

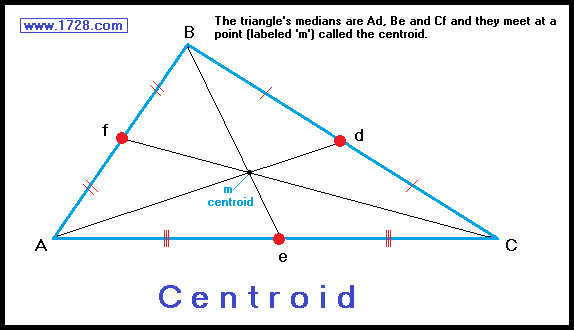
The point at which all 3 triangle medians meet is called the centroid.
(in the diagram the centroid is labeled point 'm' meaning middle).
The 6 triangles created by the medians have equal areas.
The centroid is always inside the triangle, whether it be acute, right or obtuse.
The centroid is the center of mass (the balancing point) of the triangle.

Along each median:
the distance from the vertex to the centroid is twice the distance from the centroid to the side.
Am = 2*md Bm = 2*me Cm = 2*mf

the centroid is a point 2/3 of the median distance from each vertex.
Am = ⅔ Ad Bm = ⅔ Be Cm = ⅔ Cf

the centroid is a point 1/3 of the median distance from each of the triangle's midpoints.
md = ⅓ Ad me = ⅓ Be mf = ⅓ Cf

Orthocenter

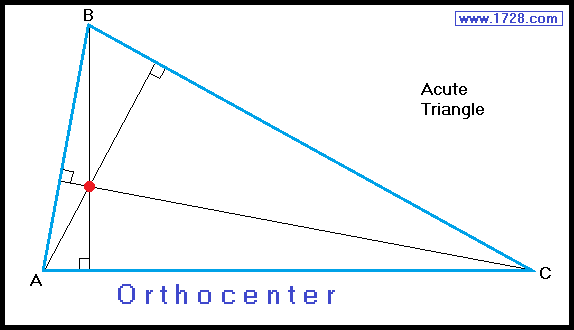
If we were to draw the altitudes of a triangle they would all meet at a point called the orthocenter.

The orthocenter of an acute triangle is always inside the triangle.
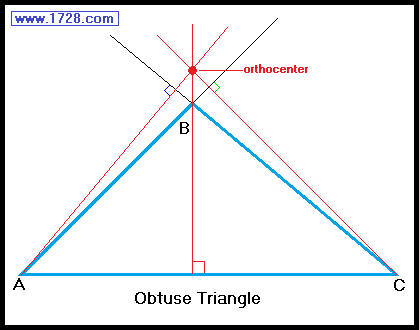
The orthocenter of an obtuse triangle is always outside the triangle and opposite the longest side.
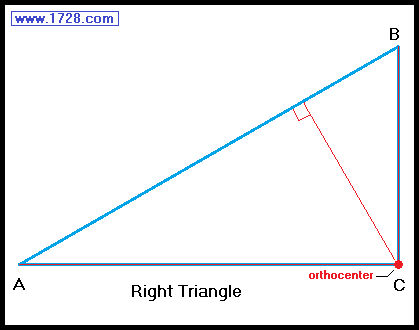
The orthocenter of a right triangle is always at the vertex of the right angle. (Also note that 2 of the "altitudes" of that triangle are sides AC and BC).

Triangle Center Summary

* * * * * * * * * Inside Triangle? Center Located at Intersection of: Center Equidistant From:

Incenter Always Angle Bisectors Triangle's Sides

Circumcenter * * * * * Perpendicular Bisectors of Sides The 3 triangle vertices

Centroid Always Medians * * * * *

Orthocenter * * * * * Altitudes * * * * *

Euler Line

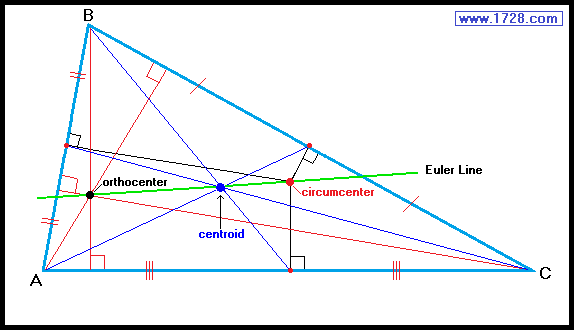
The Swiss mathematician, Leonhard Euler (1707-1783) proved that three of the triangle centers (orthocenter, centroid and circumcenter)
always lie in a straight line (called an Euler line) and the centroid is always in the middle.
The only exception is in an equilateral triangle, in which all three points, as well as the incenter, meet at the same point.
The orthocenter to centroid distance is always twice the centroid to circumcenter distance.

Return To Home Page