|
30 60 90 and 45 45 90 Triangle Calculator
Is this the length of
I N S T R U C T I O N S
Start by entering the length of a triangle side.
Then click on which type of side it is. The 5 choices you have are:
30 60 90 Triangle "Short Side", "Medium Side" or "Hypotenuse"
45 45 90 Triangle "Side" or "Hypotenuse"
As soon as you click that box, the output boxes will automatically get filled in by the calculator.
Clicking "RESET" clears all of the boxes.
Special Right Triangles
A special right triangle is one which has sides or angles for which simple formulas exist making calculations easy. Of all these special right triangles, the two encountered
most often are the 30 60 90 and the 45 45 90 triangles. For example, a speed square used by carpenters is a 45 45 90 triangle.
In the day before computers when people actually had to draw angles, special tools called drawing triangles were used and the two most popular were
the 30 60 90 and the 45 45 90 triangles.
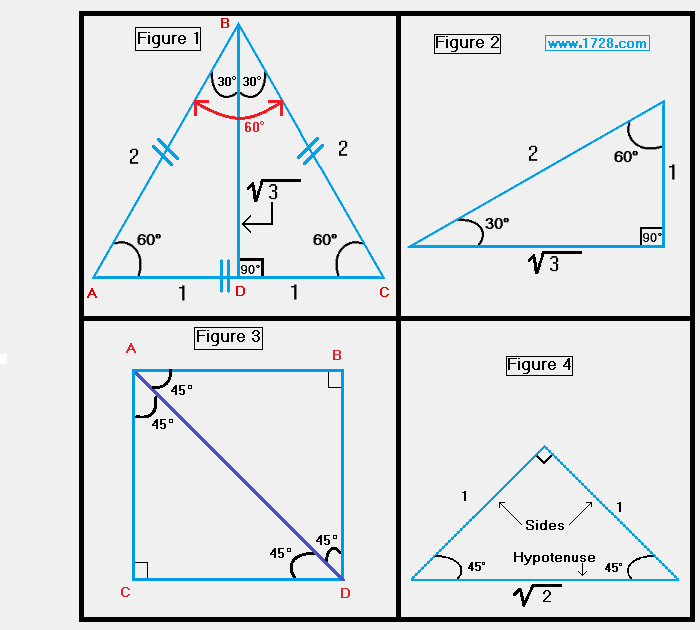
These triangles have definite geometric relationships and it would be well worth your time to study the graphics on this page to learn about the ratios of their sides. If nothing else, it is worth noting that drawing the
perpendicular bisector of an equilateral triangle (figure 1) produces a 30 60 90 triangle (figure 2) and bisecting a square along
its diagonal (figure 3) yields a 45 45 90 triangle (figure 4).
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
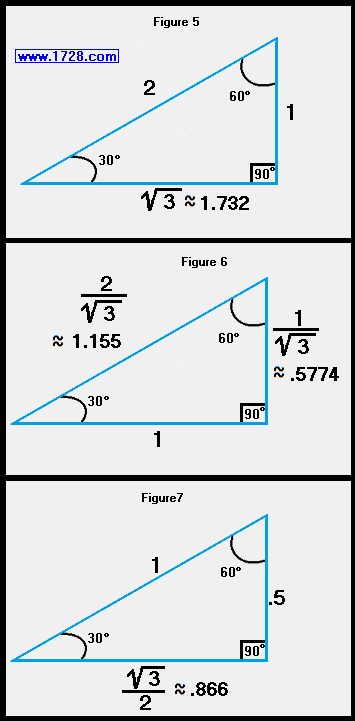
The graphics posted above show the 3 cases of a 30 60 90 triangle. If you know just 1 side of the triangle, the other 2 sides can be easily calculated.
For example, if you only know the short side (figure5), the medium side is found by multiplying this by the square root of 3 (about 1.732) and the hypotenuse is calculated by multiplying the short side by 2.
Looking at the middle section (figure 6), if you just know the "medium side", multiply this by (2 ÷ square root of 3) (about 1.155) to find the hypotenuse and multiply the medium side by (1 ÷ square root of 3) (about .5774) to calculate the short side.
The third graphic (figure 7) shows how to calculate the other sides if you only know the hypotenuse.
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
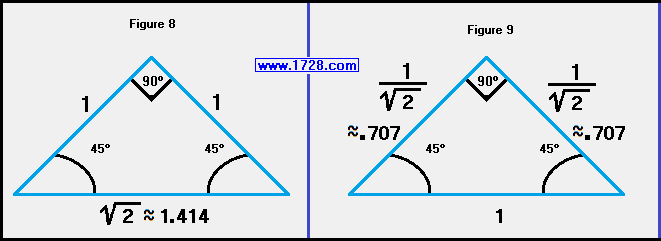
This graphic shows how to calculate the sides of a 45 45 90 triangle.
If you just know the length of one "leg" of a 45 45 90 triangle (figure 8), multiply it by the square root of 2 (about 1.414) to obtain the hypotenuse length.
If you only know the hypotenuse (figure 9), multiply this by the reciprocal of the square root of 2 (about .707) to calculate the length of the leg.
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
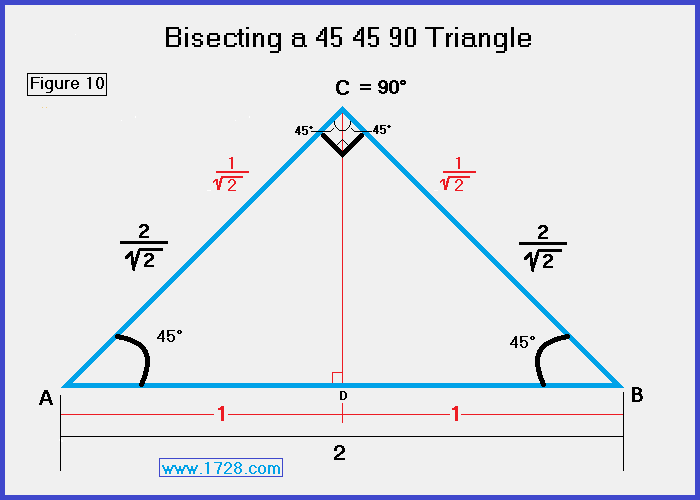Figure 10 shows what occurs when we draw the bisector of the vertex angle of a 45 45 90 triangle.
Basically, when we bisect angle C, it divides triangle ABC into two 45 45 90 triangles and it bisects side AB.
In the diagram, the text in black shows measurements before the triangle is bisected.
Numbers are displayed in scientific notation with the amount of
significant figures you specify. For easier readability, numbers between .001 and 1,000
will not be in scientific notation but will still have the same precision.
You may change the number of significant figures displayed by
changing the number in the box above.
Most browsers, will display the answers properly but
if you are seeing no answers at all, enter a zero in the box above, which will
eliminate all formatting but at least you will see the answers.
| 