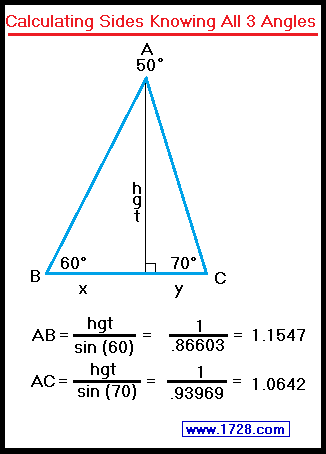
As you may already know, you can only calculate the relative lengths and NOT the actual side lengths of a triangle when you are given all 3 angles.
In spite of this, knowing the relative side lengths of a triangle can give you a good idea of what its shape will be.

As an example, let's take triangle ABC in which angle A = 50°, angle B = 60° and angle C = 70°.
We start by dropping a perpindicular from point A to side BC, and we'll say that this "height" has a length of one.
We calculate Hypotenuse AB = height ÷ sin (60°) which equals 1.1547.
Similarly, we compute hypotenuse AC equal to 1.0642.

For calculating the third side (BC), we need to use two Pythagorean Theorem equations.

side x² = 1.1547² - 1² = .33333   side x = 0.57735
side y² = 1.0642² - 1² = .13252   side y = 0.36403
Adding 0.57735 and 0.36403 we calculate side BC equals 0.94138

Let's "neaten up" those numbers just a bit, by multiplying each of those sides by the reiprocal of the shortest side.
1 ÷ .94138 = 1.06227

By doing this we get:
Side AB = 1.1547 * 1.06227 = 1.2266
Side AC = 1.0642 * 1.06227 = 1.1305
Side BC = .94138 * 1.06227 = 1

To check if your calculations are correct, go to this calculator, select "3 sides", enter 1, 1.1305 and 1.2266 then click "calculate".
Then, you'll see if your work has been done accurately.

Calculating Triangle Sides Knowing All 3 Angles
Easier Method

As an example we'll use a triangle with angles of 35°, 50° and 95°.
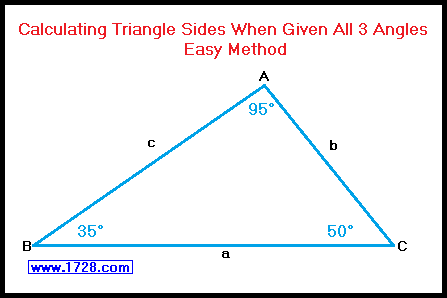Look up the sine values for each of the angles:
Sine 35° = 0.57358
Sine 50° = 0.76604
Sine 95° = 0.99619
And that's it!

Granted we could "neaten up" the numbers by multiplying them by the reciprocal of the smallest side 1 ÷ .57358 = 1.743436
0.57358 * 1.743436 =   side b =   1
0.76604 * 1.743436 =   side c =     1.33554
0.99619 * 1.743436 =   side a =     1.73679