Trigonometry Tutorial Page Two

Trigonometry Tutorial (Part 2)

Using the Law of Sines and the Law of Cosines for Solving Oblique Triangles

For solving oblique triangles without using the Law of Sines or Cosines, click here.

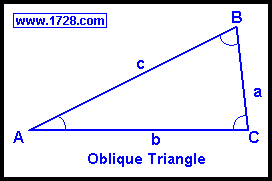An oblique triangle is one which contains no right angles.
The angles from smallest to largest are generally labeled with the uppercase letters, 'A,B & C' and each side opposite those angles is labeled with the corresponding lowercase letters 'a,b & c'.

Except for the case of knowing all 3 angles, if we know 3 properties of any triangle, we can determine the other 3.

Two Angles and One Side
Use the Law of Sines
When using the Law of Sines, remember that an ambiguous case may occur.

Angle C equals 180° - Angle A - Angle B
To find the other sides, we use the Law of Sines.

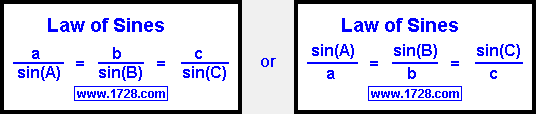Example
A triangle has 2 angles of 75° and 25° and the included side is 5. What is the other angle and the other 2 sides?
We'll say Angle A = 25°, Angle B = 75° and side c = 5.

Angle C is easily solved by 180° -75° -25° = 80°
To solve for the other sides we use the Law of Sines.
By doing a little algebra, we see that side b = (sin(B)•side c) ÷ sin(C)
side b = sin(75° • 5) ÷ sin(80°) Using the calculator to find the sine values: side b = (.96593 • 5) ÷ (.98481) side b = 4.9041 We could use the Pythagorean Theorem to solve the third side, but just for practice, let's use the Law of Sines once again.
Side a = (sin(25°) • 4.9041) ÷ sin (75°) Using the calculator to find the sine values:
Side a = (.42262 • 4.9041) ÷ .96593 Side a = 2.1457

Two Sides and a Non-Included Angle
Use the Law of Sines

When using the Law of Sines, remember that an ambiguous case may occur.

As you probably know, when solving for a triangle with 2 known sides and a non-included angle, there may be no solution, one solution or even two solutions.
In a triangle of sides 'c', 'a' and its opposite Angle 'A', the number of solutions is calculated by:
• If a < c•sin(A) no solution
• If a = c•sin(A) one solution: ∠C=90° ∠B=(90°-∠A) and side b=(c•cos(A))
• If c>a>c•sin(A) two solutions.
• If a>=c one solution
Example
A triangle has sides of 7 and 8 and a non-included angle of 60°
What are the other angles and the other side?

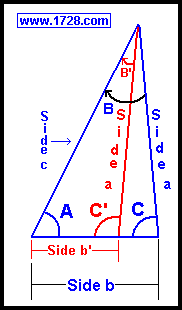Referring to the above diagram, let's say side a=7, c=8 and Angle A=60°
Using the Law of Sines to find Angle(C): sin(C)=(sin(A)•c) ÷ a sin(C)=(.86603•8) ÷ 7 Angle(C) = arc sin (.989749) = 81.789°
Angle B is easily solved by: Angle B = (180° - ∠A - ∠C)
Angle B = (180° - 60° - 81.789°) = 38.211°
Side b is found by using the Law of Sines:
side b=(7•sin(B)) ÷ sin(A) side b=(7• .61856) ÷ .86603 side b=5

If there is a second solution:
We can check to see if there is a second solution by the test:

If c>a>c•sin(A) there are 2 solutions. 8 > 7 > (8 • sin (60°)) Since 8 > 7 > 6.92824, there are two solutions.

Whenever there are two solutions in a side-side non-included triangle, ∠C will have 2 values. We will call this second value ∠C'. Angles C and C' are supplemental angles (they always add up to 180°).
So, to find the "other" angle C, use the formula:

∠(C') = 180° - ∠(C); ∠(C') = 180° - 81.789° ∠(C') = 98.213°
Using a formula very similar to the one for finding ∠(B), we find ∠(B') by:
∠(B') = 180° -∠(A) - ∠(C') ∠(B') = 180° -60° - 98.213° ∠(B') = 21.787°
Side b' is found by using the Law of Sines:
side b'=(side a •sin(B')) ÷ sin(A) side b'=(7• .37116) ÷ .86603 side b'=(2.59812) ÷ .86603 side b'=3

For a calculator and a further explanation of side-side-angle triangles, please click here.

Two Sides and the Included Angle
Use the Law of Cosines

To find the other side we use the Law of Cosines.

It is important to stress that there is only one Law of Cosines even though three "laws" have been listed. These three "laws" are not generated by algebraic manipulation. If you look at the oblique triangle graphic and each of these expressions, you will see how these three equations are derived.

Example
A triangle has sides of 4 and 9 with an included angle of 30°. What are the other 2 angles and the length of the other side?
Let's say side a=4 and side b=9 and angle C=30°

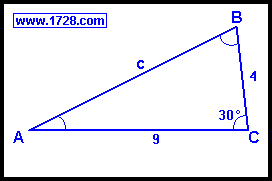From the Law of Cosines:
side c² = a² + b² -2ab • cos(C)
side c² = 4² + 9² -2•4•9 • cos(30) side c² = 16 + 81 -(72 • .86603) side c² = 34.6458 side c = 5.886
From the Law of Sines:
When using the Law of Sines, remember that an ambiguous case may occur.

sin(A) = (a*sin(C)) ÷ c sin(A) = (4*sin(30°) ÷ 9 sin(A) = 2 ÷ 5.886 sin(A) = .339785 ∠A = 19.864° Angle B is easily solved by: ∠B = 180° - ∠A - ∠C ∠B = 180° - 19.864° - 30° ∠B = 130.136

All Three Sides Of A Triangle
Use the Law of Cosines

We use the Law of Cosines when we know all three sides of a triangle.
In the graphic below, the Law of Cosines has been solved for all 3 possible angles. These equations were derived from the other Law of Cosines table but each of these equations were obtained from each of the other equations.
Basically, you cannot memorize one Law of Cosines and manipulate it algebraically to find the other two. Instead you have to see the way this applies to a triangle geometrically in order to see how the other equations are formed.

EXAMPLE:
A triangle has sides of length four, five and six. What are all 3 angles?
Let's say that side a=4, side b=5 and side c=6 and we'll first solve for Angle A.

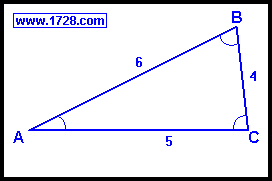cos(A) = (b² + c² -a²) ÷ (2bc) cos(A) = (5² + 6² -4²) ÷ (2•5•6) cos(A) = (25 + 36 - 16) ÷ (60) cos(A) = (.75)
Going to the calculator, we find the arc cos(.75) = 41.41°
For the second angle, we now can use an easier method, the Law of Sines.
When using the Law of Sines, remember that an ambiguous case may occur.

sin ∠B = (b • sin(A)) ÷ a sin ∠B = (5 • sin(41.41°)) ÷ 4 sin ∠B = .8268 ∠B = 55.771°
Angle C is easily found by:
∠C = 180° - ∠A -∠B ∠C = 180° -41.41° -55.771° ∠C = 82.819°

Go To Page Three
Solving Oblique Triangles Without Using Law of Sines and Law of Cosines

Go To Page One
Basic Trigonometric Functions

Return To Home Page