|
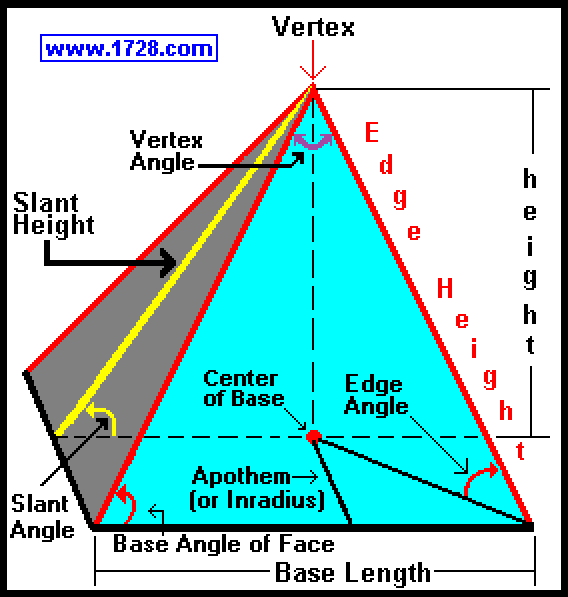
|
|
The default setting is for 5 significant figures but you can change that by inputting another number in the box above. Answers are displayed in scientific notation and for easier readability, numbers between .001 and 1,000 will be displayed in standard format (with the same number of significant figures.) The answers should display properly but there are a few browsers that will show no output whatsoever. If so, enter a zero in the box above. This eliminates all formatting but it is better than seeing no output at all.
Copyright © 1999 - 1728 Software Systems |