WORK PROBLEMS PIPE FILL PROBLEMS

Solving Algebra Work Problems
Scroll down to see Solving Algebra Pipe Filling Problems

In algebra, problems dealing with two (or more) people working together are encountered quite often. (These are quite similar to "pipes filling a pool" problems and are solved similarly.)

Example 1
Bill can paint a room in 6 hours and Dave can paint a room in 4 hours.
If they both work togeher, how much time will it take them to paint one room?
There are several ways in which this can be solved:

a) Set up rates based on time per room making sure the same time is used for each person.

In 6 hours Bill paints one room.
Dave's rate of 4 hours per room can be converted to 6 hours per 1½ rooms.
So, 2½ rooms could be painted in 6 hours, and this converts to:
6 ÷ 2½ = 2.4 hours.

b) Set up rates based on rooms per time.

In one hour, Bill paints ⅙ of a room and Dave paints ¼ of a room.
So together they paint (⅙ + ¼) = 10/24 = 5/12 of a room in one hour.
5/12 rooms per hour = 12/5 hours per room = 2.4 hours.

c) Use a formula.

Formulas are usually the best way for solving problems but memorize them exactly especially if you will be taking a test.
It might seem unusual to have a special formula to use for two people, but you have to admit it is much easier than using formula 2.

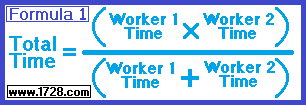
Using Formula 1 with the data from example "1"
Time = (6 * 4) ÷ (6 + 4)
Time = (24) ÷ (10)
Time = 2.4 hours.

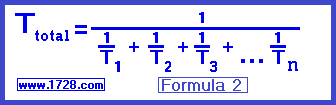
Using Formula 2
Time = 1 ÷ [(1/6) + (1/4)]
Time = 1 ÷ [(4/24) + (6/24)]
Time = 1 ÷ (10/24)
Time = 24/10
Time = 2.4 hours
See? Formula 1 is much better isn't it?

d) Use a calculator

This calculator is designed for solving parallel resistances but can also be used for these type of problems.
Just for a quick example, 4 pipes, working separately, can each fill a pool in 7, 8, 9 and 12 hours. If they all work together, how quickly will the pool be filled?
Entering these numbers into the calculator shows that the pool will be filled in 2.1631 hours.

Example 2
Two people working together can mow a lawn in 72 minutes.
When working separately, one person can mow the lawn one hour faster than the other.
How much time would it take for each person to mow the lawn when working separately?

Looking at Formula 1, let's set up equation "A" where "F" is the faster speed and "S" is the slower speed.

A) (F × S) ÷ (F + S) = 72
We know that one person is 1 hour (60 minutes) faster than the other, giving us equation "B"
B) F + 60 = S
Inserting equation B into equation A, we get:
(F × F + 60) ÷ (F + F + 60) = 72
(F² + 60F) ÷ (2F + 60) = 72
(F² + 60F) = 72 • (2F + 60)
(F² + 60F) = 144F + 4,320
F² - 84F - 4,320 = 0
Using the quadratic equation calculator, we find F = 120 and inserting this into
equation B) F + 60 = S B) 120 + 60 = S we get S =180.

Example 3
Two people can paint a room in 4 hours 48 minutes (or 4.8 hours).
If 1 person can paint the room in 12 hours, how long would it take the other person working alone?

Basically, you could do this by solving Formula 1 for either Worker 1 Time or Worker 2 Time.
But that's okay because we've done it for you.

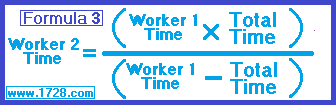
We input this information into Formula 3.
Worker 2 Time = (12 × 4.8) ÷ (12 - 4.8)
Worker 2 Time = 57.6 ÷ 7.2
Worker 2 Time = 8 hours.

* * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
Pipe Filling Problems
(or Tank Filling Problems)

Example 1
Pipe 1 can fill a tank in 3 hours and Pipe 2 can fill a tank in 4 hours.
If both pipes are turned on at the same time, how long will it take to fill the tank?

Let's determine the rate per hour for each pipe.
Pipe 1 fills ⅓ of the tank in 1 hour.
Pipe 2 fills ¼ of the tank in 1 hour.

Working together, they wiil fill how much of the tank in one hour?
(1 / 3) + (1 / 4) = (4 / 12) + (3 / 12) = 7 / 12

Seven twelfths is how much of the tank will be filled in one hour.
To get the total time, we take the reciprocal which is 12 ÷ 7 and so, the entire tank will be filled in 1.7143 hours.

When we have 2 pipes filling a tank, we can use formula "A" to calculate the total time.

Formula "B" is much easier to use and you would probably prefer to use it for 2 pipes.

Example 2
When we have 3 or more pipes filling a pool, we need to use formula "C" to calculate the total time.

For example, if we have 4 pipes that can each fill a pool in 2 hours, 3 hours, 4 hours and 6 hours, how long will it take if all 4 pipes work together?

Total Time = 1 / [ (1/2) + (1/3) + (1/4) + (1/6) ]
Total Time = 1 / [ (6/12) + (4/12) + (3/12) + (2/12) ]
Total Time = 1 / [ (15/12) ]
Total Time = (12/15) = (4/5) = .8 hours = 48 minutes.

Whenever you are calculating 3 or more pipes, it would probably be a good idea to use this parallel resistor calculator.

Example 3
Two pipes can fill a tank in 2.1 hours. One pipe working alone can fill the tank in 7 hours.
Working alone, how long would it take the other pipe to fill up the tank?

We need to use formula D for this problem.

We'll say the total time is 2.1 hours and that the Pipe 1 time is 7 hours.

Pipe 2 Time = (7 * 2.1) / (7 -2.1) = 14.7 / 4.9 = 3 hours

Example 4
We have a tank that is filled to the top.

One pipe can fill the tank in 20 minutes and the drain pipe can drain the tank in 15 minutes.
If both pipes are opened how long will it take to empty the tank?

Total Time = (20 * 15) / (20 -15) = 300 / 5 = 60 minutes

We have an empty tank.

One pipe can fill the tank in 1 hour and the drain pipe can drain the tank in 2 hours.
If the "fill" pipe is turned on while the drain pipe is open, how long will it take to fill the tank?

Once again, we will use formula "E" to calculate the total time.

Total Time = (1 * 2) / |1 -2| = 2 / 1 = 2 hours

Return To Home Page