First we need the compound interest formula which is:
Total = Principal × ( 1 + Rate )years
Now let's say the amount that we invest annually is $2,000 per year and the interest rate is 8%.
The $2,000 invested 3 years ago has become
The $2,000 invested 2 years ago has become
The $2,000 invested 1 year ago becomes
Adding up all 3 yearly amounts, we obtain $7,012.22
To make these calculations a little easier, there is a formula:
where the AMOUNT is the annual amount invested each year,
So, we have:
$2,000 * { [1.36048896 -1] ÷ .08 } — $2,000.00
$2,000 * { .36048896 ÷ .08 } — $2,000.00
$2,000 * { 4.506112 } — $2,000.00
$9,012.224 — $2,000.00
$7,012.22
Which is the answer we obtained using the "long" method at the top of this page.
2) Solving the Annual Amount
You have an 8% annual interest annuity which yields $100,000, after 25 years.
We input the amounts into the numerator:
which equals 78.954415149
Dividing 100,000 by the numerator
100,000 ÷ 78.954415149 =
1266.553615923 which rounds to
$1,266.55 per year.
You plan for your retirement by setting up an 8.5% annuity with an annual investment of $2,500 and you would like this to yield $500,000 when you retire.
Inputting these numbers into the numerator of the formula:
$2,000 * (1.08)3 = $2,000 * 1.259712 = $2,519.424
$2,000 * (1.08)2 = $2,000 * 1.1664 = $2,332.80
$2,000 * (1.08)1 = $2,000 * 1.08 = $2,160.00
As you can see, the mathematics of this can be a little cumbersome especially when the time
involved gets larger.
1) Solving the Total Amount 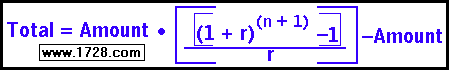
'n' is the number of years and
'r' is the annual rate of the investment.
$2,000 * { [(1 + .08)(3 + 1) -1] ÷ .08 } — $2,000.00
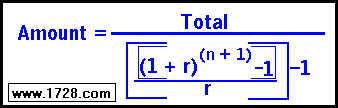
How much has to be invested each year?
([(1.08)(25 + 1)-1] ÷ .08) -1
3) Solving for Years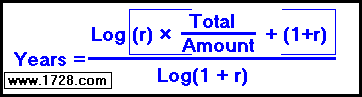
How many years will this take?
Log(.085 * (500,000 / 2500) + 1.085)
= Log(17.085)
= 1.2326149831
The log of the denominator 1.085 = 0.035429738185
The number of years = 1.2326149831 ÷ 0.035429738185
= 34.4877 years
RETURN TO ANNUITY CALCULATOR