|
.0066666666 × $100,000 × 120
1 - (1 + .0066666666) -120
Which equals:
[ .0066666666 × $100,000 × 120 ] ÷ [ 1 - (1 + .0066666666) -120 ] =
[ 80,000 ] ÷ [ 1 - (0.45052346071062) ] =
80,000 ÷ 0.54947653928939 =
$145,593.11
|
Do you want to solve for:
Input should only consist of numbers and decimal points.
Do NOT use commas, dollar signs or per cent signs.
|
Click here to go to the Loan Payment Calculator.
* * * * * * * * * * * * * * * * * * * *
Solving For Principal

The above formula is used to calculate the principal of a loan if you know the total cost, interest rate and number of payments.
We'll use the previous data.
We have paid a total of $145,593.11 for a 10 year loan at 8% interest.
What was the principal?
Using the above formula, the principal would be:
145,593.11 -145,593.11 × (1.00666666666666)-120
.00666666666666 × 120
Which Equals:
145,593.11 -(145,593.11 × 0.450523460710793) =
.8
145,593.11 -65,593.11 =
.8
100,000.00
* * * * * * * * * * * * * * * * * * * *
Solving For Number of Payments (Months)
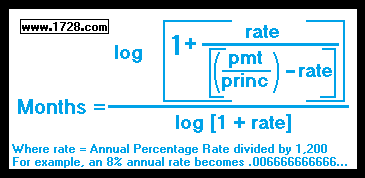
The above formula is used to calculate how many months it will take to pay off a loan if you know the principal, interest rate and the monthly payment.
We'll use the previous data.
We are paying $1,213.28 per month for a $100,000.00 loan at 8% annual interest.
How many months will it take to pay for this loan?
Looking at the formula, we see the numerator equals:
log (1 + {.006666666666 / [(1,213.28 / $100,000.00) -.006666666666]})
= log (1 + {.006666666666 / [0.0121328 -.006666666666]})
= log (1 + {.006666666666 / 0.005466133334})
= log (1 + 1.21963118338135)
= log (2.21963118338135)
numerator = 0.34628081755
denominator = log (1.0066666666)
denominator = .0028856882372
So, the time it will take equals the numerator divided by the denominator =
0.34628081755 / .0028856882372 =
120 months
|
